邻接矩阵从无权图进行改进
无权图的邻接矩阵
之前使用邻接矩阵实现的稠密图、无权图如下:
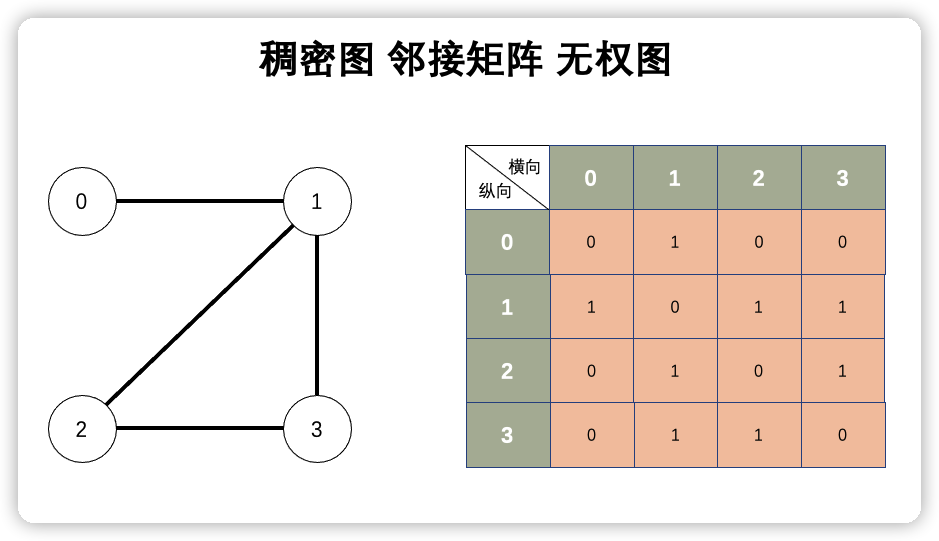
在一个 n * n 的二维数组中表示两点相连即为 1(true),不连则为 0(false)。这在无权图中好使,但是如果是有权图,比如下:
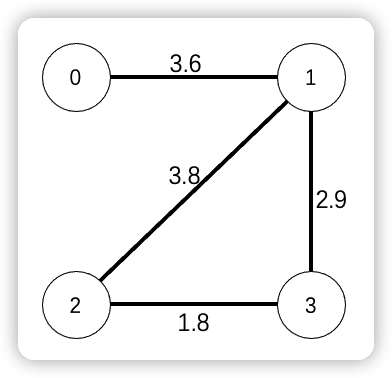
这中间已经不止存在着连接关系了,还有权值,这里的权值如:3.6、3.8、2.9、1.8。这些权值可能表示着距离、时间等等,在复杂点可能不是数字,而是一个对象,所以不能再像无权图那样简单的使用 0、1 表示。
Edge
单独抽象出来一个 边类型,起名 Edge,属性包含了 两个相连接的点、权重,权重使用模板,具体是什么类型让使用者决定。
#include <iostream>
#include <cassert>
/**
* 有权图的 边 模板类
*/
template<typename Weight>
class Edge {
private:
/**
* 边相连的两个顶点
*
* 无向图,谁在前谁在后无所谓
* 有向图,规定 a 在前
*/
int a, b;
/** 权重 */
Weight weight;
public:
Edge() {}
Edge(int a, int b, Weight weight) {
this->a = a;
this->b = b;
this->weight = weight;
}
~Edge() {}
/** 获取顶点 a */
int v() {
return a;
}
/** 获取顶点 b */
int w() {
return b;
}
/** 获取权重 */
Weight wt() {
return weight;
}
/** 获取边上指定点的另一个点 */
int other(int x) {
assert(x == a || x == b);
return x == a ? b : a;
}
friend std::ostream &operator<<(std::ostream &os, Edge<Weight> &e) {
os << e.v() << "-" << e.w() << ": " << e.wt();
return os;
}
bool operator<(Edge<Weight>& e) {
return weight < e.wt();
}
bool operator<=(Edge<Weight>& e) {
return weight <= e.wt();
}
bool operator>(Edge<Weight>& e) {
return weight > e.wt();
}
bool operator>=(Edge<Weight>& e) {
return weight >= e.wt();
}
bool operator==(Edge<Weight>& e) {
return weight == e.wt();
}
};有权图的邻接矩阵
在增加了 Edge 类之后,就变成了如下图:
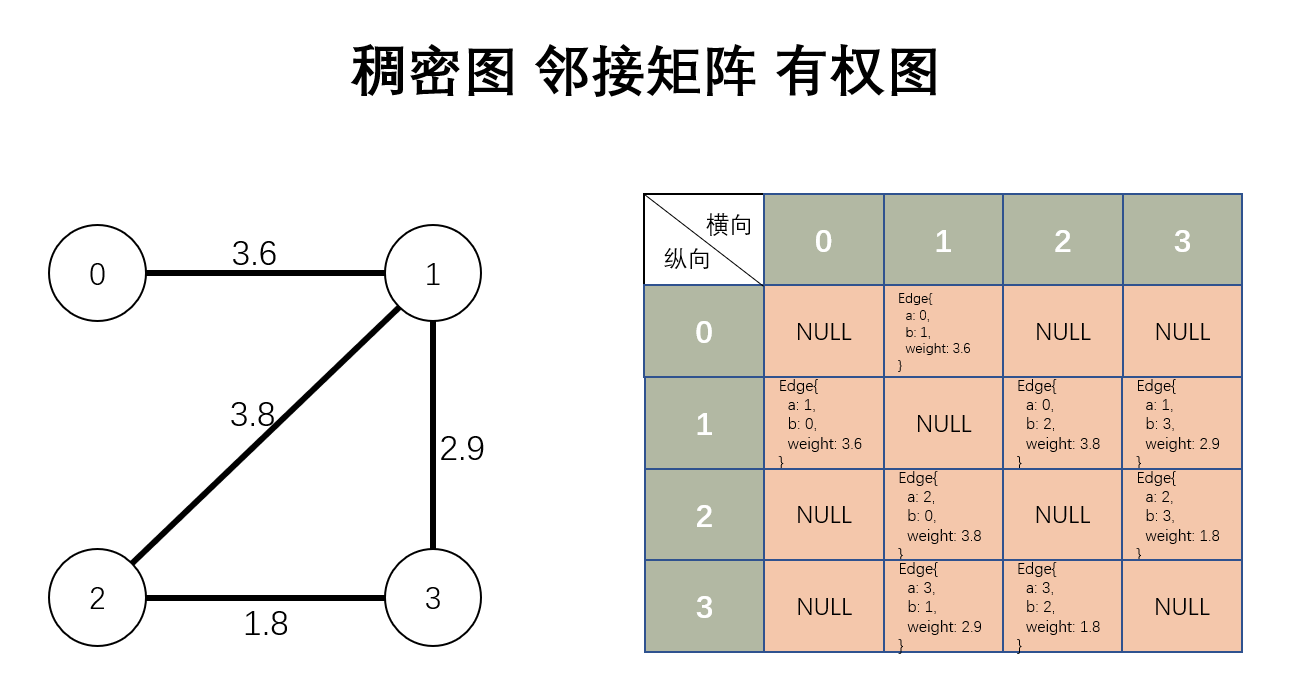
实现
#include <iostream>
#include <cassert>
#include <vector>
#include "Edge.h"
/**
* 稠密图,有权图 - 邻接矩阵
*/
template<typename Weight>
class DenseGraph {
private:
/**
* 图中顶点数、边数
*/
int n, m;
/**
* 是否为有向图
*/
bool directed;
/**
* 矩阵,由于改成有权图了,所以不能单纯的使用 true、false 标识是否连接
* 还需要 Weight 表示边的权重
*/
std::vector<std::vector<Edge<Weight> *>> g;
public:
DenseGraph(int n, bool directed) {
this->n = n;
this->m = 0;
this->directed = directed;
for (int i = 0; i < n; ++i) {
// 创建一个 n * n 的矩阵,每一排
// g 中总共有 n 行
// 每行总共有 n 个元素,每个元素默认为 NULL,未有任何连接
g.push_back(std::vector<Edge<Weight> *>(n, nullptr));
}
}
~DenseGraph() {
// 由于边都是 new 出来的,遍历删除掉
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (g[i][j]) {
delete g[i][j];
}
}
}
}
/**
* 图中有多少顶点
*
* @return 顶点的个数
*/
int v() {
return n;
}
/**
* 图中有多少边
*
* @return 边的个数
*/
int e() {
return m;
}
/**
* 连接 v 和 w,在他们之间建立一条边
*
* 平行边:v 和 w 都是唯一的,不存在平行边
* 自环边:当 v 和 w 一样时,稠密图天生只会存在一个自环边
*
* @param weight 边的权重
*/
void addEdge(int v, int w, Weight weight) {
assert(v >= 0 && v < n);
assert(w >= 0 && w < n);
if (hasEdge(v, w)) {
// 已经存在边了,重复的连接操作
// 但是有可能新的 weight 权重更优
// 这里可以根据不同业务做不同比较。
// 测试代码就直接把原来的删除,进行新增
delete g[v][w];
if (!directed) {
delete g[w][v];
}
// 删除后维护 m
--m;
}
g[v][w] = new Edge<Weight>(v, w, weight);
if (!directed) {
// 无向图
g[w][v] = new Edge<Weight>(w, v, weight);
}
++m;
}
/**
* 两顶点之间是否存在边
*
* 时间复杂度:O(1)
*/
bool hasEdge(int v, int w) {
assert(v >= 0 && v < n);
assert(w >= 0 && w < n);
return g[v][w];
};
/**
* 显示图的信息
*/
void show() {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (g[i][j]) {
// 显示边的权重
std::cout << g[i][j]->wt() << "\t";
} else {
std::cout << "NULL" << "\t";
}
}
std::cout << std::endl;
}
}
/**
* 邻边迭代器
*/
class AdjIterator {
private:
DenseGraph &G;
/** 顶点 */
int v;
/** 当前迭代到第几个 */
int index;
public:
AdjIterator(DenseGraph &graph, int v) : G(graph) {
this->v = v;
this->index = 0;
}
/**
* 稠密图中,每一行的第 0 个元素不一定是相连的,要为 true 才为相连
*/
Edge<Weight> *begin() {
index = -1;
return next();
}
Edge<Weight> *next() {
// 只要 index 还小于顶点总数(稠密图中行和列数都是顶点总数),就可以继续向下查询
for (index += 1; index < G.v(); ++index) {
if (G.g[v][index]) {
return G.g[v][index];
}
}
return nullptr;
}
bool end() {
return index >= G.v();
}
};
};测试
// testG1.txt
8 16
4 5 .35
4 7 .37
5 7 .28
0 7 .16
1 5 .32
0 4 .38
2 3 .17
1 7 .19
0 2 .26
1 2 .36
1 3 .29
2 7 .34
6 2 .40
3 6 .52
6 0 .58
6 4 .93组成图为如下:
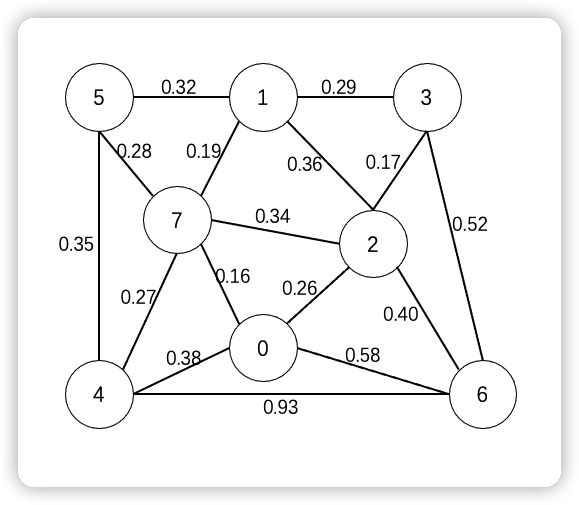
void testRead() {
string filename = "testG1.txt";
int v = 8;
// 小数点两位
cout << fixed << setprecision(2);
// Test Weighted Dense Graph
DenseGraph<double> g1 = DenseGraph<double>(v, false);
ReadGraph<DenseGraph<double>, double> readGraph1(g1, filename);
g1.show();
cout << endl;
}show:
NULL NULL 0.26 NULL 0.38 NULL 0.58 0.16
NULL NULL 0.36 0.29 NULL 0.32 NULL 0.19
0.26 0.36 NULL 0.17 NULL NULL 0.40 0.34
NULL 0.29 0.17 NULL NULL NULL 0.52 NULL
0.38 NULL NULL NULL NULL 0.35 0.93 0.37
NULL 0.32 NULL NULL 0.35 NULL NULL 0.28
0.58 NULL 0.40 0.52 0.93 NULL NULL NULL
0.16 0.19 0.34 NULL 0.37 0.28 NULL NULL 邻接表从无权图进行改进
部分内容在上面稠密图中已经说过,不再过多赘述。
无权图的邻接表
之前使用邻接表实现的稀疏图、无权图如下:
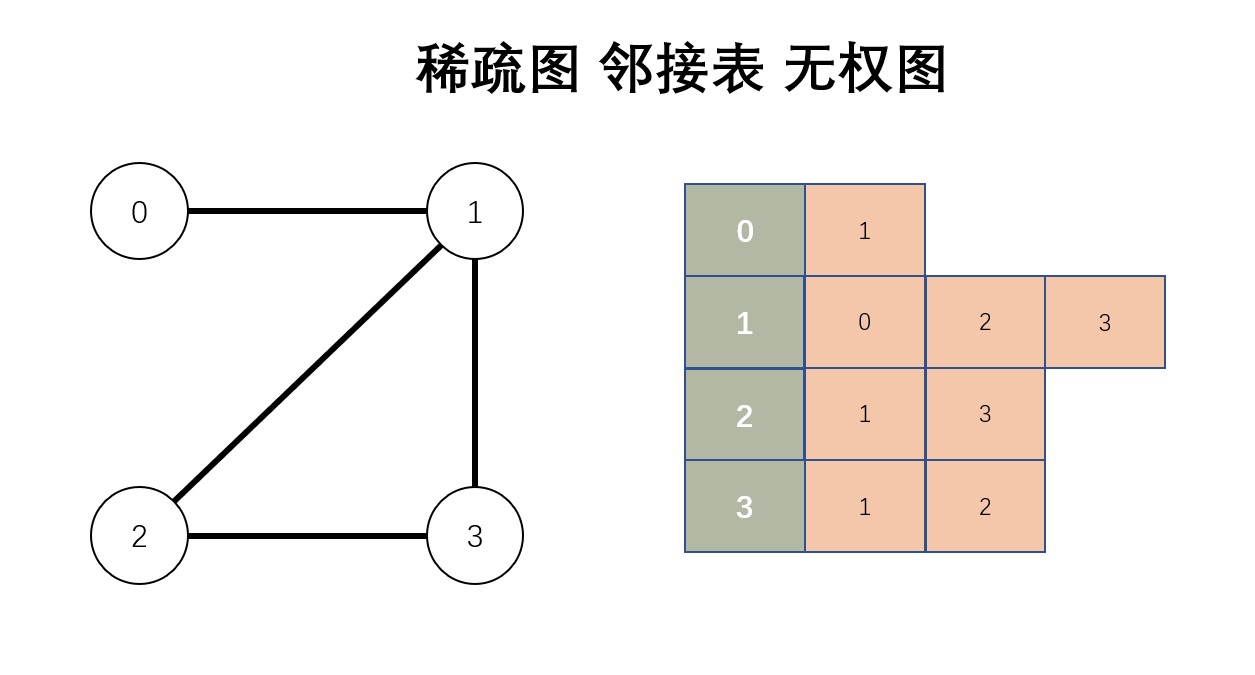
有权图的邻接表
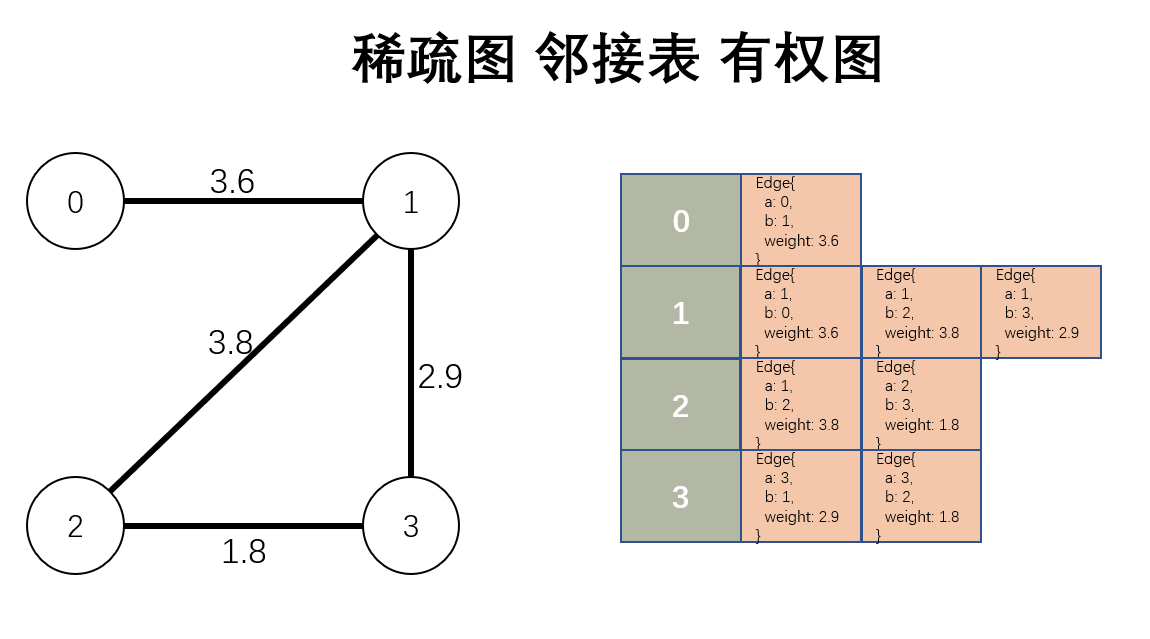
实现
#include <iostream>
#include <cassert>
#include <vector>
#include "Edge.h"
/**
* 稀疏图,有权图 - 邻接表
*/
template<typename Weight>
class SparseGraph {
private:
/**
* 图中顶点数、边数
*/
int n, m;
/**
* 是否为有向图
*/
bool directed;
/**
* 邻接表,每行存放的都是当前行所连接的所有顶点
*/
std::vector<std::vector<Edge<Weight> *>> g;
public:
SparseGraph(int n, bool directed) {
this->n = n;
this->m = 0;
this->directed = directed;
g = std::vector<std::vector<Edge<Weight> *>>(n, std::vector<Edge<Weight> *>());
}
~SparseGraph() {
for (int i = 0; i < n; ++i) {
for (int j = 0; j < g[i].size(); ++j) {
delete g[i][j];
}
}
}
/**
* 图中有多少顶点
*
* @return 顶点的个数
*/
int v() {
return n;
}
/**
* 图中有多少边
*
* @return 边的个数
*/
int e() {
return m;
}
/**
* 连接 v 和 w,在他们之间建立一条边
*
* 平行边:存在平行边的情况,如果添加的时候想过滤平行边,就需要调用 hasEdge 进行判断,那 addEdge 就变成了 O(n) 时间复杂度
* 一般不在 addEdge 时处理,在所有边都添加完毕之后再去重。
* 自环边:当 v 和 w 一样时,并且是无向图时,就会存在添加两次自环边的情况,所以要判断筛选掉
*
* @param weight 边的权重
*/
void addEdge(int v, int w, Weight weight) {
assert(v >= 0 && v < n);
assert(w >= 0 && w < n);
g[v].push_back(new Edge<Weight>(v, w, weight));
if (v != w && !directed) {
// 无向图
g[w].push_back(new Edge<Weight>(w, v, weight));
}
++m;
}
/**
* 两顶点之间是否存在边
*
* 时间复杂度:O(n)
*/
bool hasEdge(int v, int w) {
assert(v >= 0 && v < n);
assert(w >= 0 && w < n);
for (int i = 0; i < g[v].size(); ++i) {
// 到这里,遍历的所有边中有一点肯定是 v,只需要看另一点是否为 w 即可。
if (g[v][i]->other(v) == w) {
return true;
}
}
return false;
}
/**
* 显示图的信息
*/
void show() {
for (int i = 0; i < n; i++) {
std::cout << "vertex " << i << ":\t";
for (int j = 0; j < g[i].size(); j++) {
std::cout << "( to:" << g[i][j]->w() << ",wt:" << g[i][j]->wt() << ")\t";
}
std::cout << std::endl;
}
}
/**
* 邻边迭代器
*/
class AdjIterator {
private:
SparseGraph &G;
/** 顶点 */
int v;
/** 当前迭代到第几个 */
int index;
public:
AdjIterator(SparseGraph &graph, int v) : G(graph) {
this->v = v;
this->index = 0;
}
Edge<Weight> *begin() {
index = 0;
// size 大于 0
if (G.g[v].size()) {
return G.g[v][index];
}
return nullptr;
}
Edge<Weight> *next() {
++index;
if (index < G.g[v].size()) {
return G.g[v][index];
}
return nullptr;
}
bool end() {
return index >= G.g[v].size();
}
};
};测试
void testRead() {
string filename = "testG1.txt";
int v = 8;
// 小数点两位
cout << fixed << setprecision(2);
// Test Weighted Sparse Graph
SparseGraph<double> g2 = SparseGraph<double>(v, false);
ReadGraph<SparseGraph<double>, double> readGraph2(g2, filename);
g2.show();
cout << endl;
}show:
vertex 0: ( to:7,wt:0.16) ( to:4,wt:0.38) ( to:2,wt:0.26) ( to:6,wt:0.58)
vertex 1: ( to:5,wt:0.32) ( to:7,wt:0.19) ( to:2,wt:0.36) ( to:3,wt:0.29)
vertex 2: ( to:3,wt:0.17) ( to:0,wt:0.26) ( to:1,wt:0.36) ( to:7,wt:0.34) ( to:6,wt:0.40)
vertex 3: ( to:2,wt:0.17) ( to:1,wt:0.29) ( to:6,wt:0.52)
vertex 4: ( to:5,wt:0.35) ( to:7,wt:0.37) ( to:0,wt:0.38) ( to:6,wt:0.93)
vertex 5: ( to:4,wt:0.35) ( to:7,wt:0.28) ( to:1,wt:0.32)
vertex 6: ( to:2,wt:0.40) ( to:3,wt:0.52) ( to:0,wt:0.58) ( to:4,wt:0.93)
vertex 7: ( to:4,wt:0.37) ( to:5,wt:0.28) ( to:0,wt:0.16) ( to:1,wt:0.19) ( to:2,wt:0.34)
文章评论