简介

迪杰斯特拉算法(Dijkstra) 是由荷兰计算机科学家狄克斯特拉于1959年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。

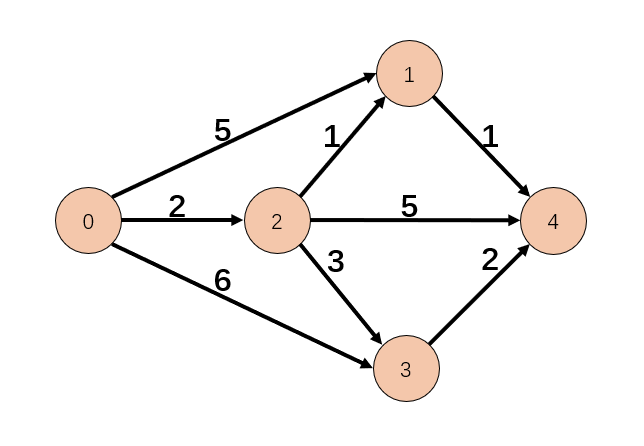
注意，Dijkstra 算法无法处理负权边的情况，比如 0 到 2 点的距离为：-2。

松弛操作（Relaxation）

何为松弛操作，文字描述比较抽象，看图吧。

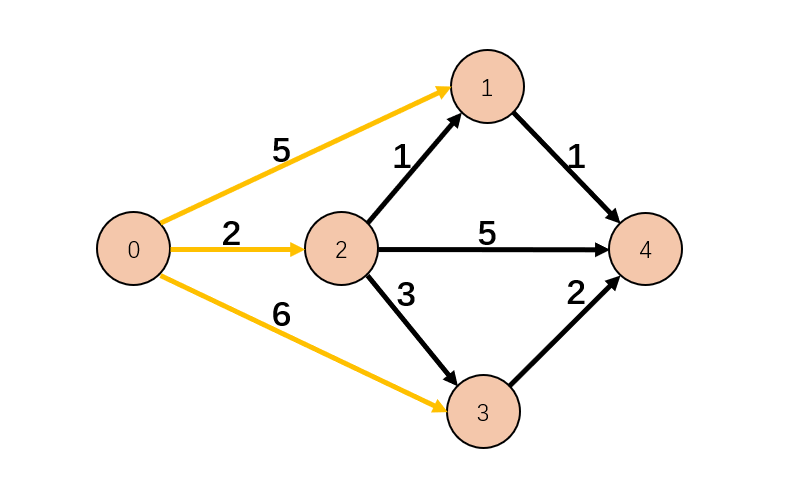
0 的邻点有 1、2、3，距离分别是 5、2、6，这其中，距离最短的是 2，到点 2，那么就可以推断出 0 到 2 的距离肯定是最短的。为什么？假设还有一条边从 1 到 2 的。

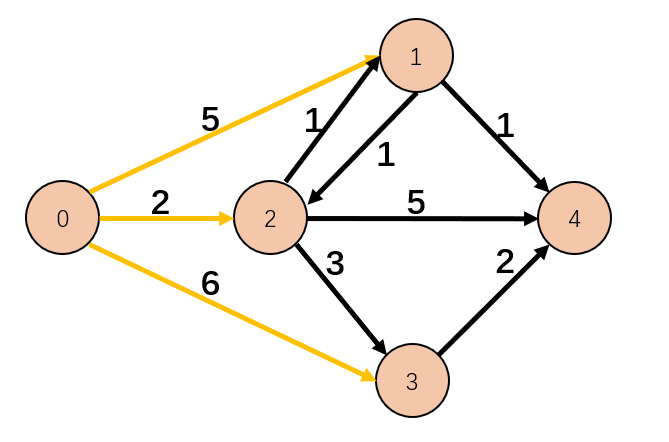
路径 0 - 1 的距离是 5，就光这一条边的距离已经超过了 0 - 2 的距离 2 了，再从 1 连接到 2，距离是 1，那总距离是 6，肯定没有 0 - 2 的距离短。那 0 - 3 - 2 就更不用说了，0 - 3 的距离已经是 6 了。

注意：以上都是不存在负权边的情况，假设 1 - 2 的距离是 -4，那就不一样了。Dijkstra 不能处理负权边。

松弛操作

上边已经找到 0 - 2 是第一次查找的最短路径，开始以 2 为基础进行松弛操作。

遍历点 2 的邻点，查看以点 2 为基础距离（现在到点 2 的基础距离为 2），再加上点 2 到其邻点的距离，是否比原来已知的能到达邻点的距离短。如下图：

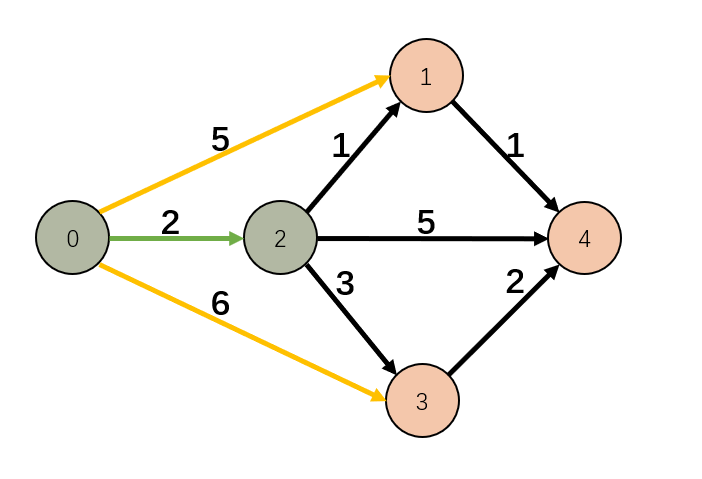
• 2 - 1 的距离为 1，再加上点 2 的基础距离 2，得出 0 - 2 - 1 的总距离为：3。
• 原到点 1 的距离是 0 - 1 的距离 5，显然此次松弛操作后，0 - 2 - 1 的距离是更短的，把到点 1 的距离更新为：3。
• 2 - 3 的距离为 3，再加上点 2 的基础距离 2，得出 0 - 2 - 3 的总距离为：5。
• 原到点 3 的距离是 0 - 1 的距离 6，显然此次松弛操作后，0 - 2 - 3 的距离是更短的，把到点 1 的距离更新为：5。
• ......

总结来说就是找到一个已经确定了为最短路径的点，这里就是点 2，以其为基础距离，看其到邻点的距离是否更优。更优则更新，否则跳过。

实现

0 到其他点的最短距离动画演示

先以 0 为起点到其他所有点的最短距离观察一下。

代码实现

#include <iostream>
#include <vector>
#include <stack>
#include "../help/Edge.h"
#include "IndexMinHeap.h"

/**
 * Dijkstra 算法求最短路径
 *
 * 时间复杂度：O(Elog(V))
 */
template<typename Graph, typename Weight>
class Dijkstra {
private:
    /**
     * 图
     */
    Graph &G;
    /**
     * 起始点
     */
    int s;
    /**
     * 存放已探索到的点，从 s 到这些点的距离
     */
    Weight *distTo;
    /**
     * 点是否已经找到了最短路径
     */
    bool *marked;
    /**
     * 记录当前点是从那个点过来的
     * 通过此字段可以反推 s 到任一点的最短路径
     */
    vector<Edge<Weight> *> from;
    /**
     * 在松弛过后用来获取已探索路径中最短的点
     */
    IndexMinHeap<Weight> ipq;

public:
    Dijkstra(Graph &graph, int s) : G(graph), ipq(IndexMinHeap<Weight>(graph.v())) {
        assert( s >= 0 && s < G.v() );

        // 初始化成员变量
        this->s = s;
        distTo = new Weight[G.v()];
        marked = new bool[G.v()];
        for (int i = 0; i < graph.v(); ++i) {
            distTo[i] = Weight();
            marked[i] = false;
            from.push_back(nullptr);
        }

        // 因为从 s 点开始，s 点的就可以固定初始化一下
        // 到 s 点的上一个点也是 s 自己。
        from[s] = new Edge<Weight>(s, s, Weight());
        // 把 s 放入已探索最小索引堆，等待取出
        ipq.insert(s, Weight());

        while (!ipq.isEmpty()) {
            Weight v = ipq.extractMinIndex();
            // 新取出的已探索最短距离点必然是最短路径
            marked[v] = true;

            // 遍历 v 的邻边进行松弛操作。
            typename Graph::AdjIterator adjIter(G, v);
            for (Edge<Weight> *e = adjIter.begin(); !adjIter.end(); e = adjIter.next()) {
                // 获取当前这条边与 v 相连的点
                int w = e->other(v);

                // 点 w 没有被标记过"已经找到最短历经"的情况下再继续
                if (!marked[w]) {
                    // 如果点 w 没有被探索过 || 已经被探索过，但是新的路径距离更短
                    if (nullptr == from[w] || distTo[v] + e->wt() < distTo[w]) {
                        from[w] = e;
                        distTo[w] = distTo[v] + e->wt();

                        if (ipq.contain(w)) {
                            // 更新索引堆中的路径距离
                            ipq.change(w, distTo[w]);
                        } else {
                            // 新增
                            ipq.insert(w, distTo[w]);
                        }
                    }
                }
            }
        }
    }

    ~Dijkstra() {
        delete[] distTo;
        delete[] marked;
        delete from[s];
    }

    /**
     * 返回从 s 点到 w 点的最短路径长度
     */
    Weight shortestPathTo(int w) {
        assert(w >= 0 && w < G.v());
        assert(hasPathTo(w));
        return distTo[w];
    }

    /**
     * 判断从 s 点到 w 点是否联通
     */
    bool hasPathTo(int w) {
        assert(w >= 0 && w < G.v());
        return marked[w];
    }

    /**
     * 寻找从 s 到 w 的最短路径, 将整个路径经过的边存放在 vec 中
     */
    void shortestPath(int w, vector<Edge<Weight>> &vec) {

        assert(w >= 0 && w < G.v());
        assert(hasPathTo(w));

        // 通过from数组逆向查找到从s到w的路径, 存放到栈中
        stack<Edge<Weight> *> s;
        Edge<Weight> *e = from[w];
        while (e->v() != this->s) {
            s.push(e);
            e = from[e->v()];
        }
        s.push(e);

        // 从栈中依次取出元素, 获得顺序的从s到w的路径
        while (!s.empty()) {
            e = s.top();
            vec.push_back(*e);
            s.pop();
        }
    }

    /**
     * 打印出从 s 点到 w 点的路径
     */
    void showPath(int w) {

        assert(w >= 0 && w < G.v());
        assert(hasPathTo(w));

        vector<Edge<Weight>> vec;
        shortestPath(w, vec);
        for (int i = 0; i < vec.size(); i++) {
            cout << vec[i].v() << " -> ";
            if (i == vec.size() - 1)
                cout << vec[i].w() << endl;
        }
    }
};

测试

// testG1.txt
5 8
0 1 5
0 2 2
0 3 6
1 4 1
2 1 1
2 4 5
2 3 3
3 4 2

void testDijkstra() {
    string filename = "testG1.txt";
    int v = 5;

    SparseGraph<int> g = SparseGraph<int>(v, true);
    // Dijkstra最短路径算法同样适用于有向图
    // SparseGraph<int> g = SparseGraph<int>(v, false);
    ReadGraph<SparseGraph<int>, int> readGraph(g, filename);

    cout << "Test Dijkstra:" << endl << endl;
    Dijkstra<SparseGraph<int>, int> dij(g, 0);
    for (int i = 0; i < v; i++) {
        if (dij.hasPathTo(i)) {
            cout << "Shortest Path to " << i << " : " << dij.shortestPathTo(i) << endl;
            dij.showPath(i);
        } else
            cout << "No Path to " << i << endl;

        cout << "----------" << endl;
    }
}

show:

Test Dijkstra:

Shortest Path to 0 : 0
0 -> 0
----------
Shortest Path to 1 : 3
0 -> 2 -> 1
----------
Shortest Path to 2 : 2
0 -> 2
----------
Shortest Path to 3 : 5
0 -> 2 -> 3
----------
Shortest Path to 4 : 4
0 -> 2 -> 1 -> 4
----------