Kruskal

Kruskal 是一个简单、易于理解的算法，效率比 Prim 低，对要求不高的场景可以使用。

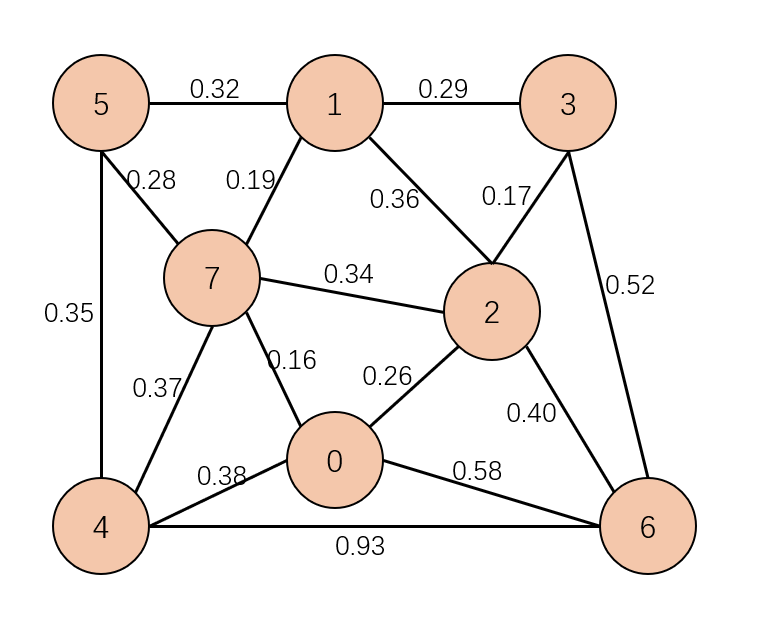
先把所有边进行排序（从小到大），开始遍历。
从遍历中挨个从小到大取出边，如果这条边被选为了最小生成树，是否会形成环？

如果会形成环就不能选定这条边。不能形成环，那就可以选定为最小生成树中的一员。
直至循环结束。

循环也可以不必到最后一个索引，只需判断选中边达到 点数 - 1 即可。

以上的关键点在于要判断两点之间的边如果被选中了，是否会形成环？这里可以使用 Union Find 在遍历的过程中把已经相连的点进行并操作，而是否可以进行相连（选中这条边作为最小生成树的一员）就要看两点是否已经在一个并集上，如果在，则不能相连，因为会形成环，否则可以相连，并进行并操作。

动画演示

代码实现

#include <vector>
#include "MinHeap.h"
#include "UnionFind.h"
#include "../help/Edge.h"

/**
 * Kruskal 算法计算最小生成树
 */
template<typename Graph, typename Weight>
class KruskalMST {
private:
    /** 用来排序所有边权重的最小堆排序 */
    MinHeap<Edge<Weight>> pq;
    /** 用来把已访问的点进行连接的并查集 */
    UnionFind uf;
    /** 记录最小生成树包含的所有边 */
    std::vector<Edge<Weight>> mst;
    /** 最小生成树的权值和 */
    Weight mstWeight;

public:
    KruskalMST(Graph &graph) : pq(MinHeap<Edge<Weight>>(graph.e())), uf(UnionFind(graph.v())) {
        // 遍历图中所有的边，放入最小堆中备用
        // 遍历所有点
        for (int i = 0; i < graph.v(); ++i) {
            // 遍历点对应的边
            typename Graph::AdjIterator adjIter(graph, i);
            for (Edge<Weight> *e = adjIter.begin(); !adjIter.end(); e = adjIter.next()) {
                // 由于是处理无向图，在无向图中，比如 1 点和 2 点相连，那就会存在两条边，1-2 和 2-1。
                // 所以此处做个筛选，只取其一
                if (e->v() < e->w()) {
                    // 这种情况只会取 1-2 的这条边
                    pq.insert(*e);
                }
            }
        }

        // 只要堆中还存在边，就可以遍历下去；优化方式：增加已选中边还小鱼 总点数 - 1。当达到 总点数 - 1 时说明已经选完了。
        while (!pq.isEmpty() && mst.size() < graph.v() - 1) {
            // 取最小边
            Edge<Weight> e = pq.extractMin();
            // 查看边的两点是否已访问过
            if (uf.isConnected(e.v(), e.w())) {
                // 两点都已经访问过，如果再选中这条边当做最小生成树，就会形成环，所以跳过
                continue;
            }

            mst.push_back(e);
            uf.unionElements(e.v(), e.w());
        }

        mstWeight = mst[0].wt();
        for (int i = 1; i < mst.size(); i++) {
            mstWeight += mst[i].wt();
        }
    }

    ~KruskalMST(){ }

    /**
     * 返回最小生成树的所有边
     */
    vector<Edge<Weight>> mstEdges(){
        return mst;
    };

    /**
     * 返回最小生成树的权值
     */
    Weight result(){
        return mstWeight;
    };
};

测试

// testG1.txt
8 16
4 5 .35
4 7 .37
5 7 .28
0 7 .16
1 5 .32
0 4 .38
2 3 .17
1 7 .19
0 2 .26
1 2 .36
1 3 .29
2 7 .34
6 2 .40
3 6 .52
6 0 .58
6 4 .93

void testKruskal() {
    string filename = "testG1.txt";
    int v = 8;

    SparseGraph<double> g = SparseGraph<double>(v, false);
    ReadGraph<SparseGraph<double>, double> readGraph(g, filename);

    // Test Kruskal MST
    cout << "Test Kruskal MST:" << endl;
    KruskalMST<SparseGraph<double>, double> kruskalMST(g);
    vector<Edge<double>> mst = kruskalMST.mstEdges();
    for (int i = 0; i < mst.size(); i++)
        cout << mst[i] << endl;
    cout << "The MST weight is: " << kruskalMST.result() << endl;

    cout << endl;
}

show:

Test Kruskal MST:
0-7: 0.16
2-3: 0.17
1-7: 0.19
0-2: 0.26
5-7: 0.28
4-5: 0.35
2-6: 0.4
The MST weight is: 1.81

最小生成树 - Kruskal

Kruskal

动画演示

代码实现

测试

文章评论