图论基本概念

简介

图是用来对 对象之间 的成对关系建模的数学结构，由 节点 或 顶点(Vertex) 以及连接这些顶点的 边(Edge) 组成。

值得注意的是，图的顶点集合不能为空，但边的集合可以为空，通俗的讲，一张图，没有点不行，没有边可以，大不了点与点之间不相连。图可能是无向的，这意味着图中的边在连接顶点时无需区分方向。否则，称图是有向的。下面左图是一个典型的无向图结构，右图则属于有向图，无向图也可以看成是一种特殊的有向图。

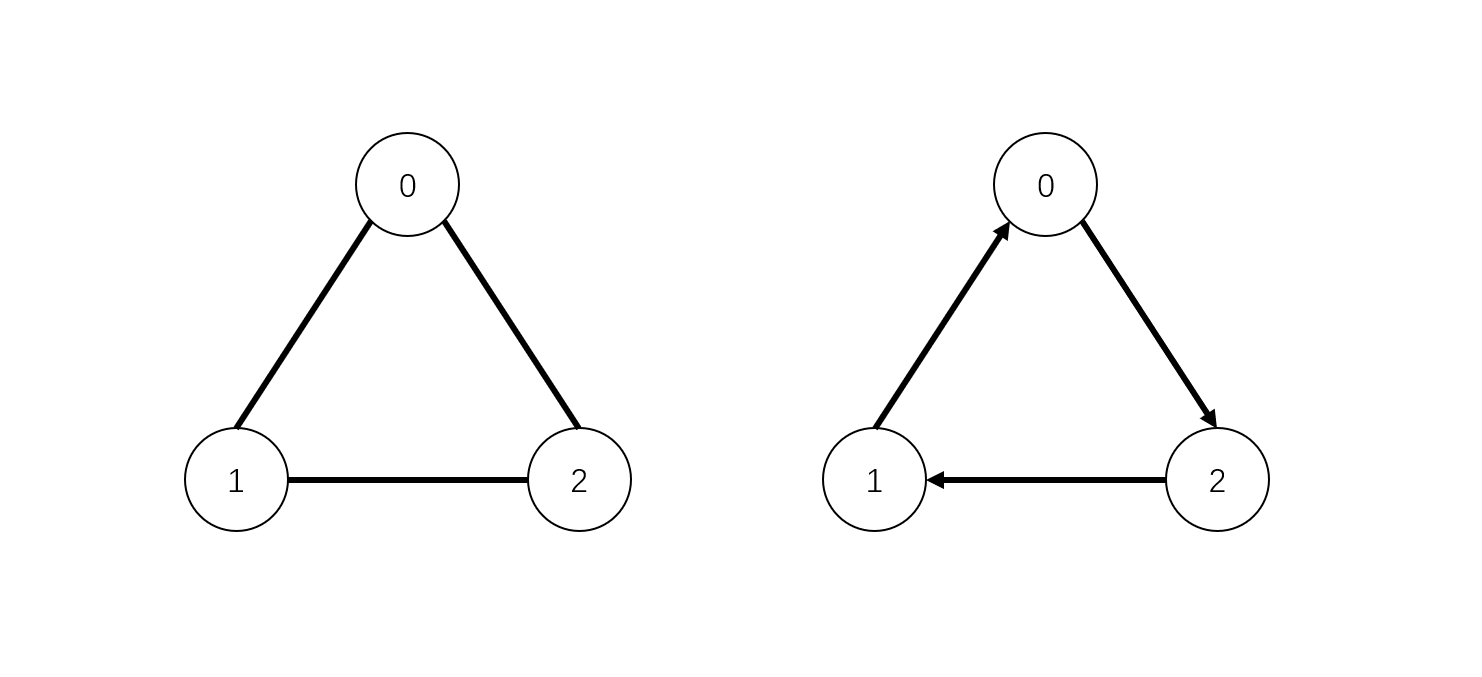
图的分类：

无权图、有权图

连接顶点与顶点的边是否有数值与之对应，有的话就是有权图，否则就是无权图。

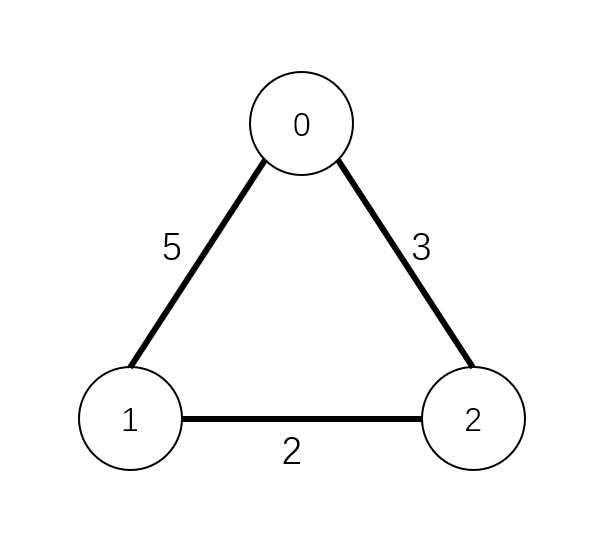
图的连通性

在一个无向图 G 中，若从顶点 i 到顶点 j 有路径相连（当然从 j 到 i 也一定有路径），则称 i 和 j 是连通的。如果 G 是有向图，那么连接 i 和 j 的路径中所有的边都必须同向。如果图中任意两点都是连通的，那么图被称作连通图。如果此图是有向图，则称为强连通图（注意：需要双向都有路径）。图的连通性是图的基本性质。在一张图中，有多少没有连接到一起的子图就有多少连通分量，如下图，存在两个连通分量。

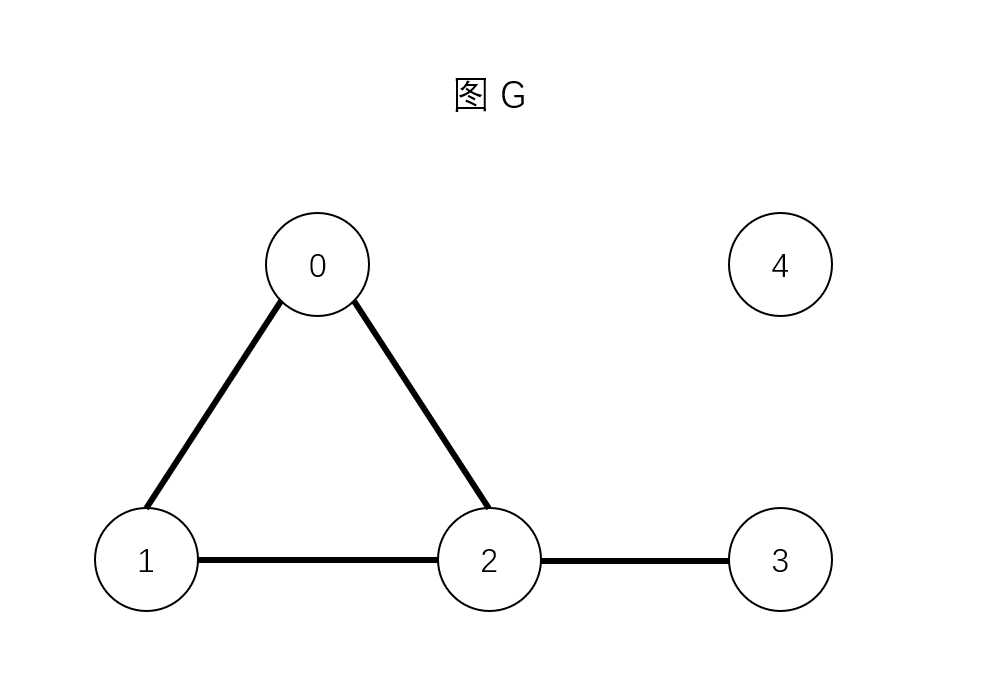
0 和 3 是连通的，1 和 3 是连通的，2 和 4 是不连通的。

完全图

其中每对不同的顶点之间都恰连有一条边相连。假设有 N 个顶点，那每个顶点的边都是 N - 1 条

自环边

一条边的起点终点是一个点。

平行边

两个顶点之间存在多条边相连接。

图的表达形式

邻接矩阵

列一个横竖长度都为所有顶点数量的二维数组（表格），表示了顶点与其他所有顶点的相连信息，包括顶点自身，矩阵本身成斜对角对称。两两相连为 1，否则为 0。

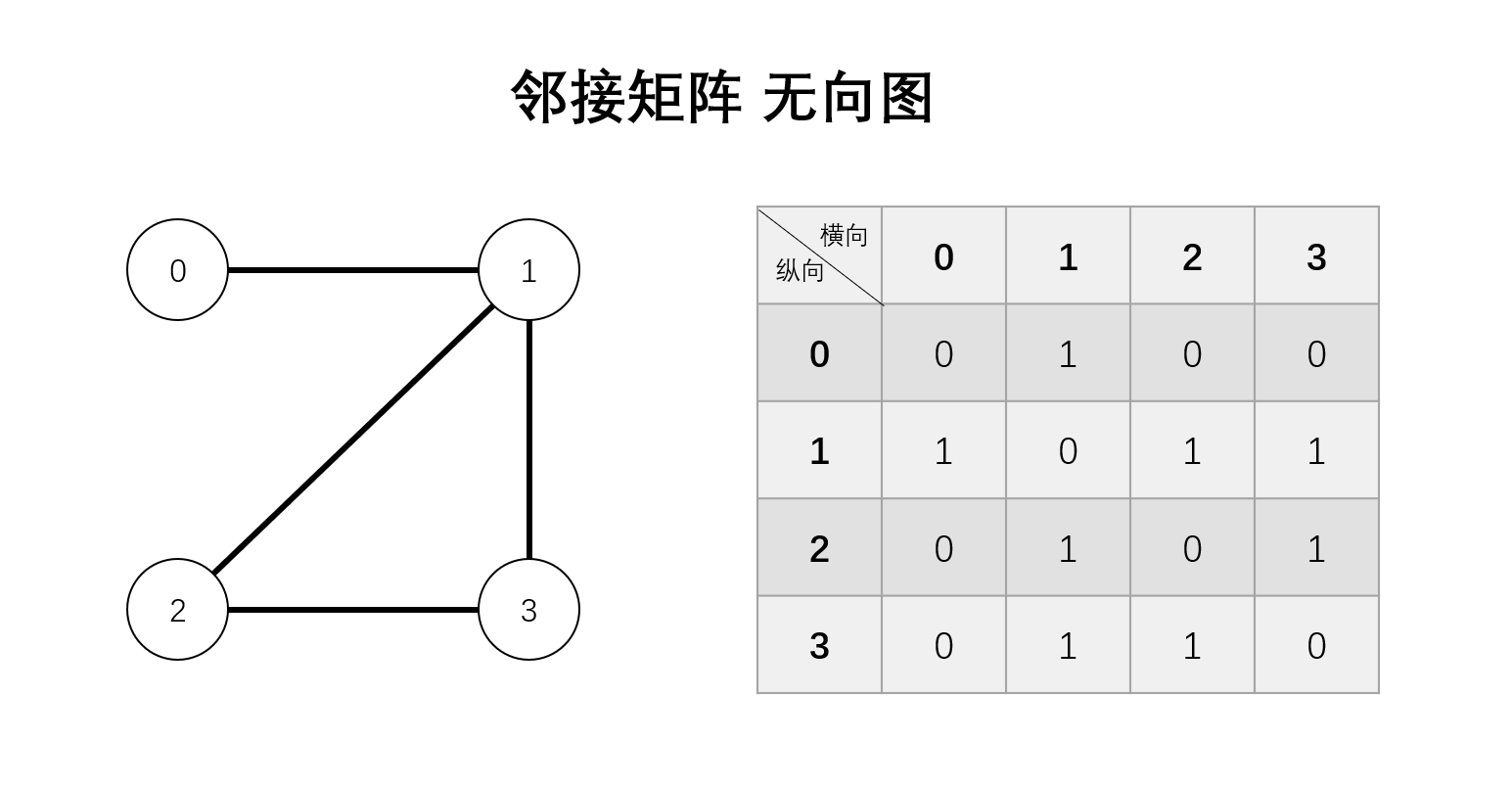
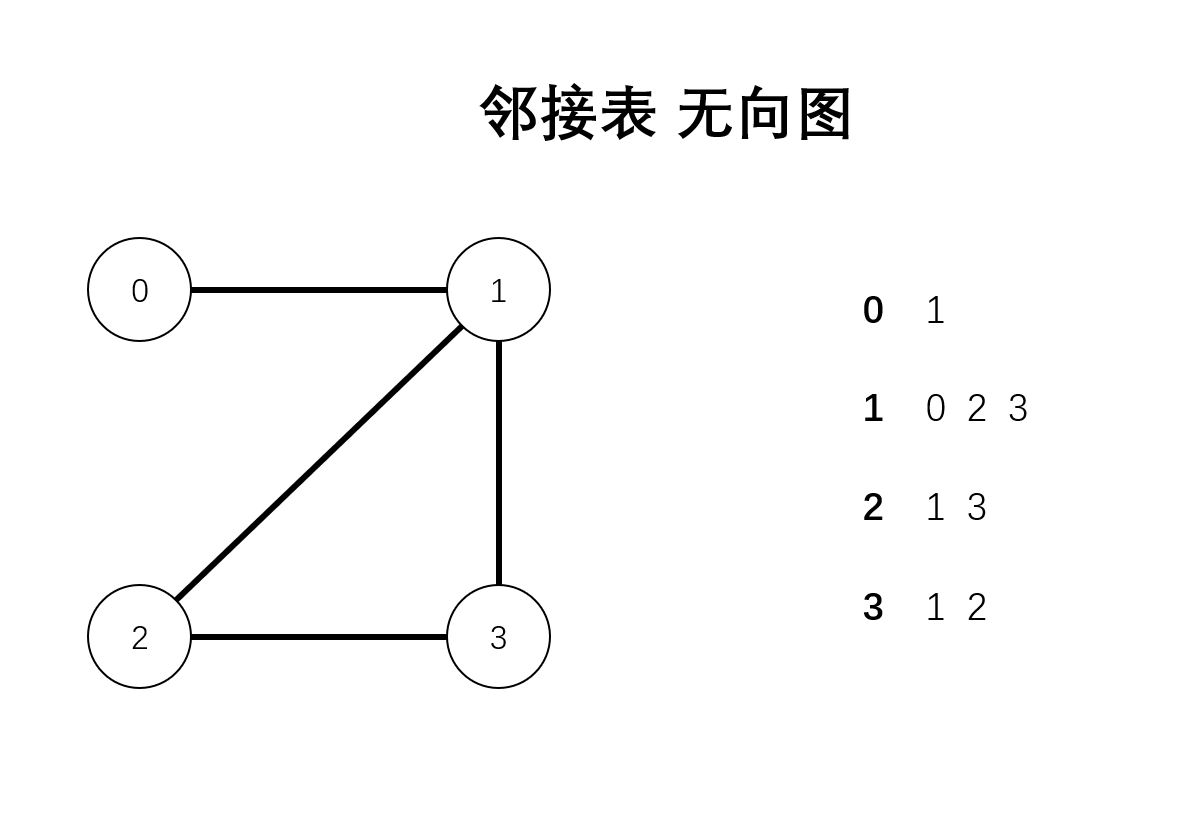
邻接表

邻接表中只表示出了顶点与其相连的顶点信息。与哪个顶点相连，就记录哪个。

适用场景

邻接矩阵适合于稠密图，邻接表适合于稀疏图。对于稠密图和稀疏图并没有广义上的明确定义。

稠密图：在一个图中，假设有 N 个顶点，每个顶点边的数量越靠近 N - 1，就越趋近于稠密图，如果每个顶点边的数量都是 N - 1 的话（完全图），也就是每个顶点都与其他所有顶点相连，那肯定是一个稠密图。
稀疏图：在一个图中，假设有 N 个顶点，每个顶点边的数量越靠近 1 甚至是 0，就越趋近于稀疏图，如果每个顶点边的数量都是 1 的话，也就是每个顶点都仅仅与其他一个顶点相连，那肯定是一个稀疏图。