广度遍历路径规划

简介

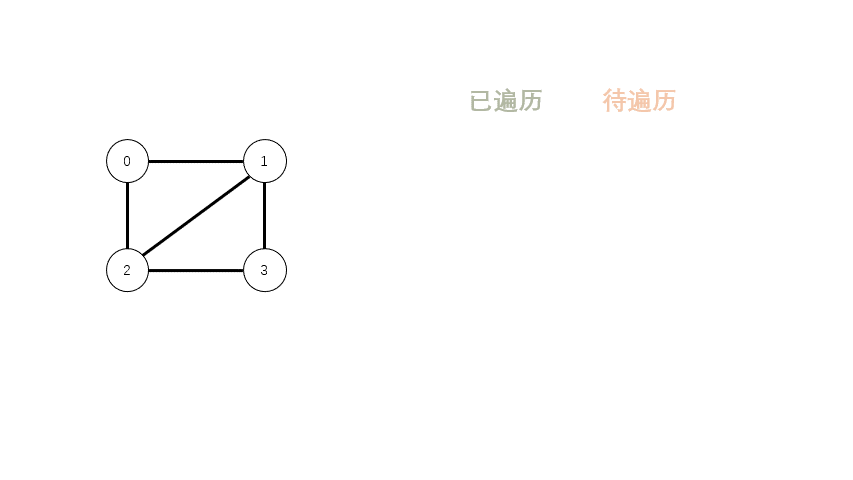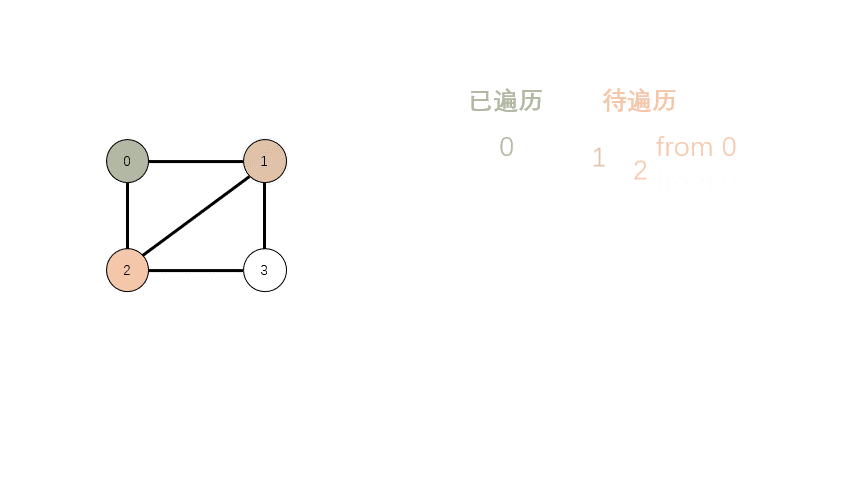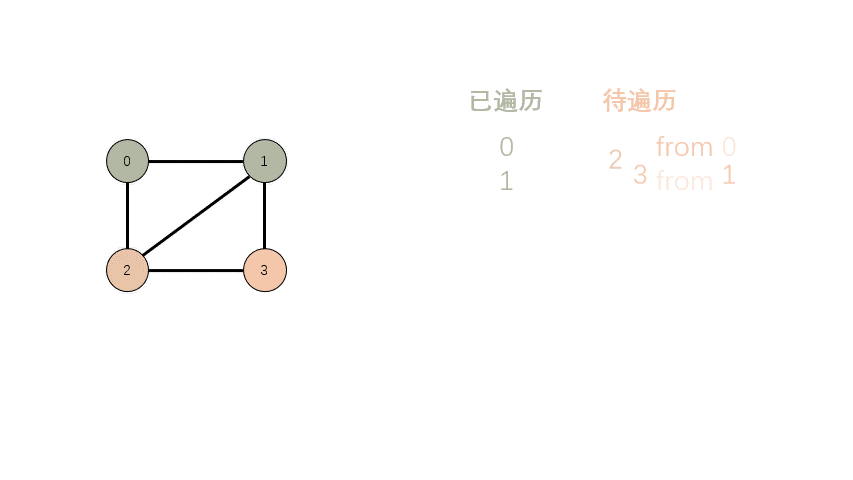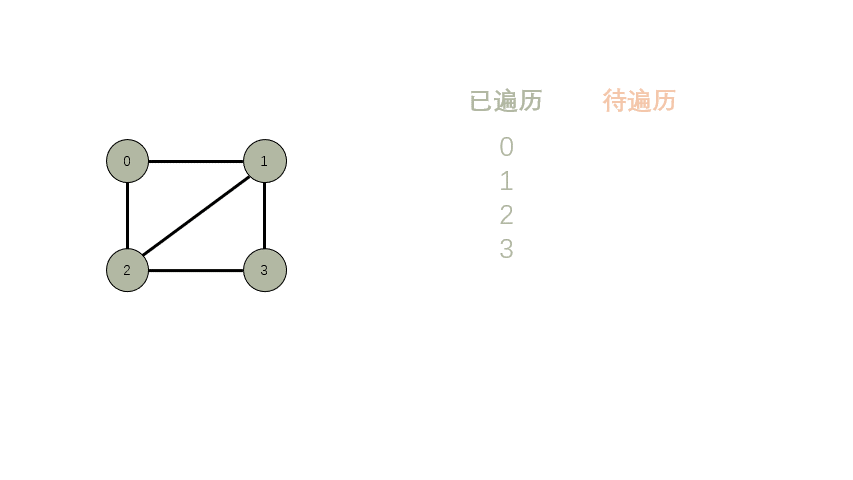
1. 增加队列，用来存放待遍历的顶点。
2. 先把起始顶点扔进队列。
3. 从队列中取出第一个顶点，遍历其相邻顶点。
   1. 如果已经遍历过 或者 已经是在队列中等待遍历了，跳过。
   2. 否则就加入队列，等待遍历。
4. 持续 3，直到没有待遍历的顶点。

广度遍历可以求最短路径。

实现

#include <iostream>
#include <vector>
#include <stack>
#include <queue>

/**
 * 广度遍历求最短路径
 *
 * 时间复杂度：
 *  稀疏图：O(V + E)
 *  稠密图：O(V^2)
 */
template<typename Graph>
class ShortestPath {
private:
    /** 图 */
    Graph &G;
    /** 在广度遍历时，是否访问过了 */
    bool *visited;
    /** 源点、起始点 */
    int s;
    /**
     * 当前顶点是从哪个顶点过来的
     * 索引为当前顶点，值为当前顶点的上一个顶点
     */
    int *from;
    /**
     * 记录顶点距离 源点的距离
     */
    int *ord;

public:
    ShortestPath(Graph &graph, int s) : G(graph) {
        visited = new bool[G.v()];
        from = new int[G.v()];
        ord = new int[G.v()];

        // 初始化时，所有顶点都没有被访问过。
        for (int i = 0; i < G.v(); ++i) {
            visited[i] = false;
            from[i] = -1;
            ord[i] = -1;
        }
        this->s = s;

        // 开始广度遍历顶点，源点的 from 为 -1。
        // 创建待遍历队列
        std::queue<int> q;
        // 先把源点扔进去
        q.push(s);
        // 标记为已遍历或者待遍历
        visited[s] = true;
        // 起始点距离起始点的距离肯定是 0
        ord[s] = 0;

        // 开始遍历队列
        while (!q.empty()) {
            // 取得队列中第一个的顶点
            int v = q.front();
            q.pop();
            // 遍历顶点的邻边并添加到队列
            typename Graph::AdjIterator adjIter(G, v);
            for (int i = adjIter.begin(); !adjIter.end(); i = adjIter.next()) {
                // 当前邻边必须是没有遍历过 并且 不在在待遍历中了
                if (!visited[i]) {
                    // 可以入队列
                    q.push(i);
                    // 标记为已遍历或者待遍历
                    visited[i] = true;
                    // 从 v 来到 i
                    from[i] = v;
                    // 记录 i 距离起始点的距离
                    ord[i] = ord[v] + 1;
                }
            }
        }

    }

    ~ShortestPath() {
        delete[] visited;
        delete[] from;
    }

    /**
     * 查看源点 与 w 顶点之间是否存在路径
     *
     * 如果 w 被遍历过，说明在一个连通分量中，肯定是存在路径的。
     */
    bool hasPath(int w) {
        assert(w >= 0 && w < G.v());

        return visited[w];
    }

    /**
     * 获取源点到 w 顶点的路径
     */
    void path(int w, std::vector<int> &vector) {
        assert(hasPath(w));

        std::stack<int> s;

        int p = w;
        while (p != -1) {
            // 只要 p 不等于 -1，说明还没倒推到源点（源点的 from 是 -1），就 push 到栈中
            s.push(p);
            p = from[p];
        }

        vector.clear();
        while (!s.empty()) {
            vector.push_back(s.top());
            s.pop();
        }
    }

    /**
     * 打印路径
     */
    void showPath(int w) {
        assert(hasPath(w));

        std::vector<int> vec;
        path(w, vec);
        for (int i = 0; i < vec.size(); i++) {
            std::cout << vec[i];
            if (i == vec.size() - 1)
                std::cout << std::endl;
            else
                std::cout << " -> ";
        }
    }

    /**
     * 查看源点到顶点 w 的距离
     */
    int length(int w) {
        assert(hasPath(w));

        return ord[w];
    }
};

测试

void testPath() {
    string filename = "testG2.txt";
    SparseGraph g = SparseGraph(7, false);
    ReadGraph<SparseGraph> readGraph(g, filename);
    g.show();

    ShortestPath<SparseGraph> bfs(g, 0);
    cout << "BFS : ";
    bfs.showPath(6);
}

// testG2.txt
7 8
0 1
0 2
0 5
0 6
3 4
3 5
4 5
4 6