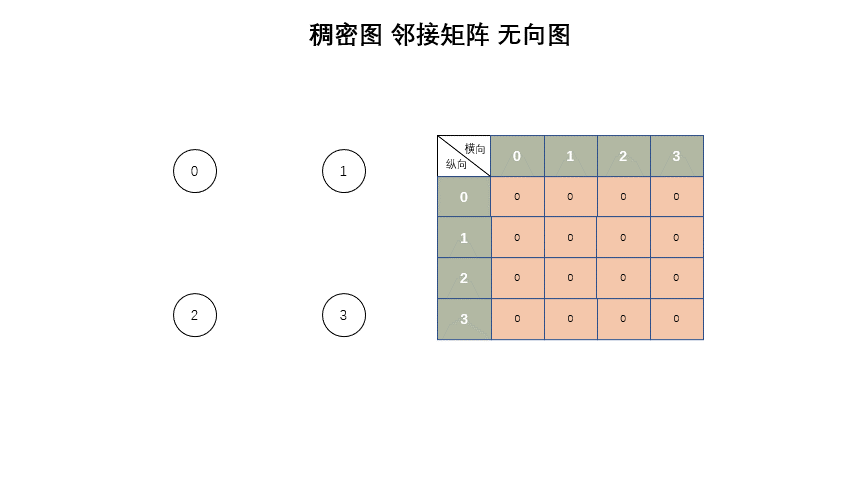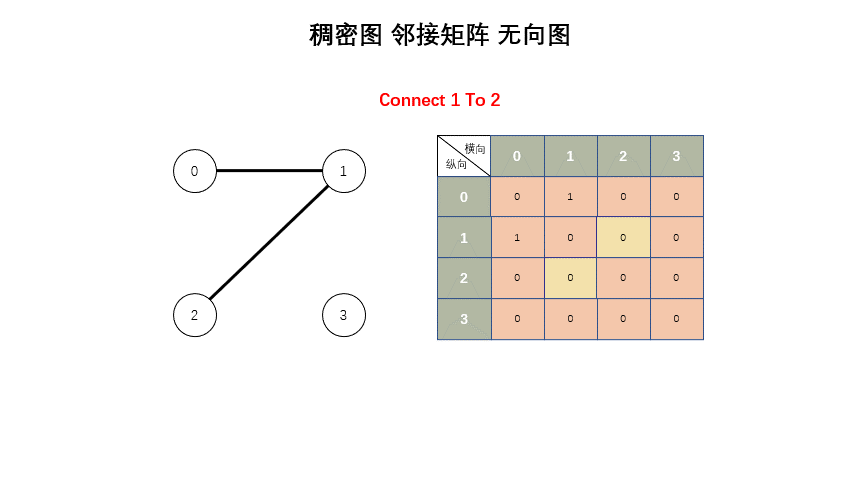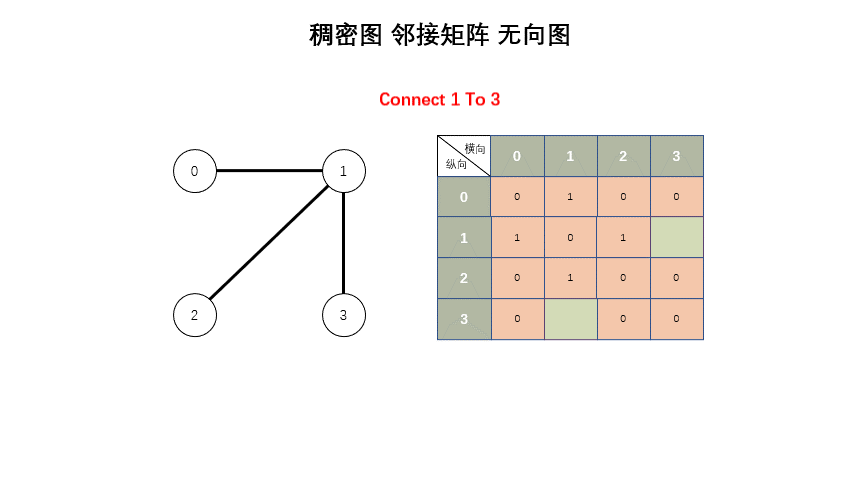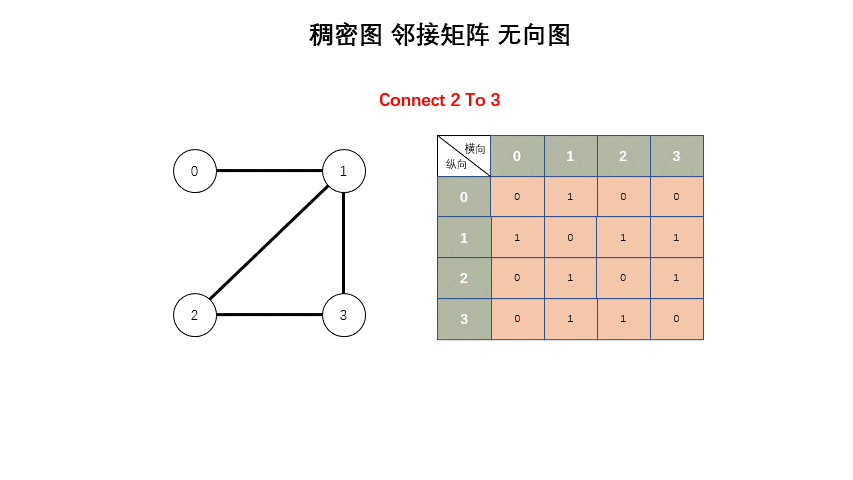
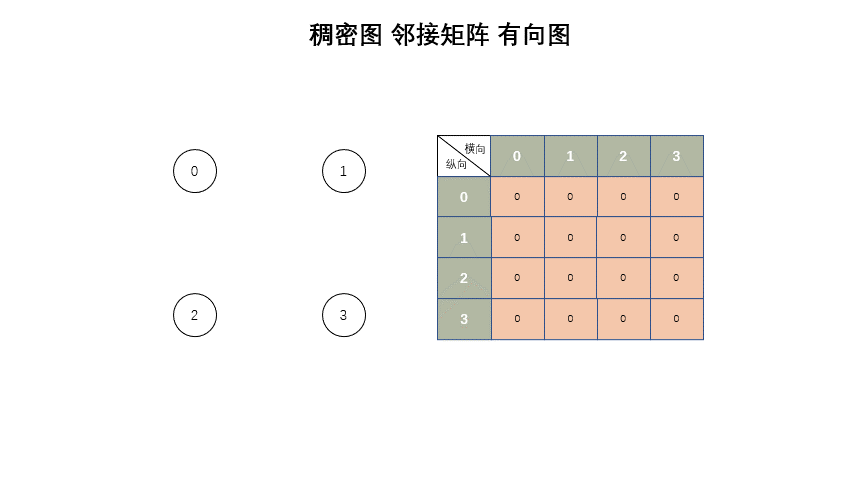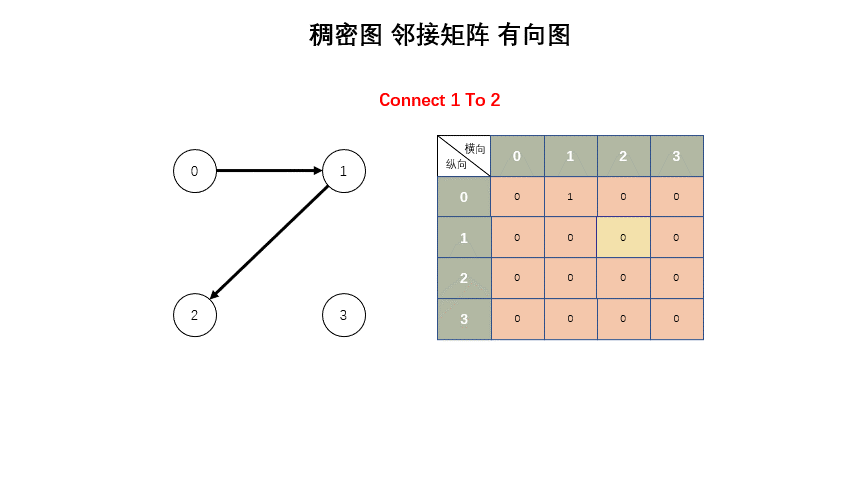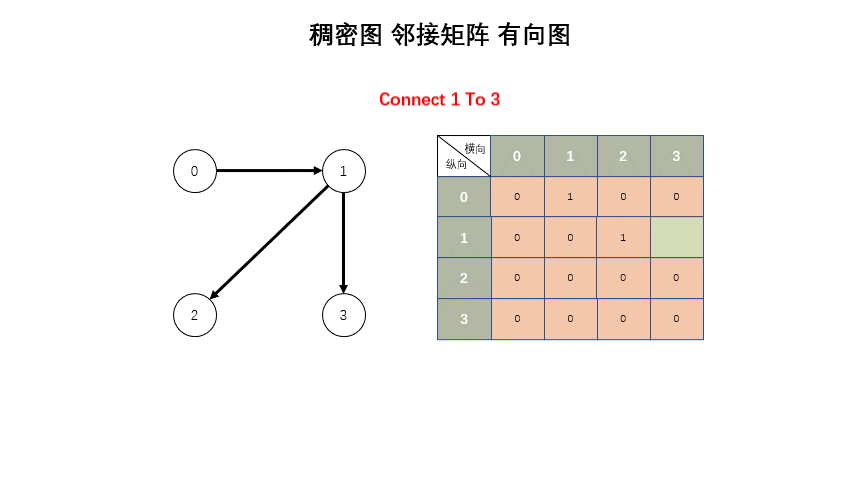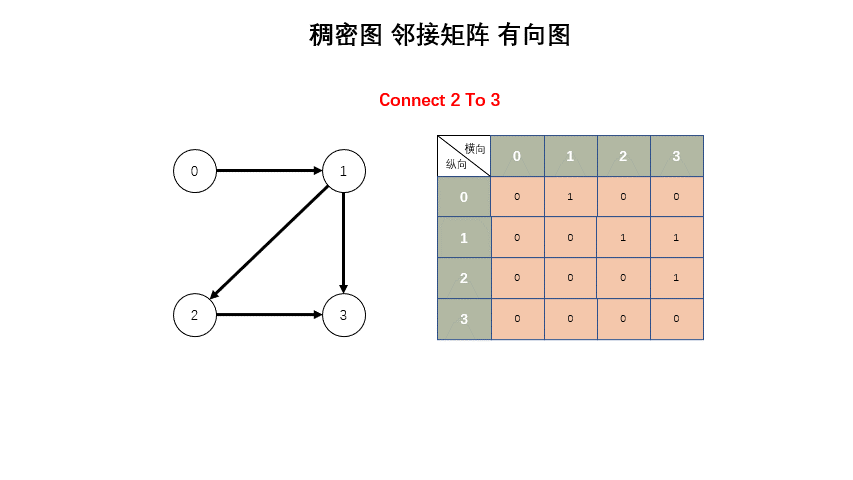
稠密图
#include <iostream>
#include <cassert>
#include <vector>
/**
* 稠密图 - 邻接矩阵
*/
class DenseGraph {
private:
/**
* 图中顶点数、边数
*/
int n, m;
/**
* 是否为有向图
*/
bool directed;
/**
* 矩阵,有边就是 true,无边就是 false。
*/
std::vector<std::vector<bool>> g;
public:
DenseGraph(int n, bool directed) {
this->n = n;
this->m = 0;
this->directed = directed;
for (int i = 0; i < n; ++i) {
// 创建一个 n * n 的矩阵,每一排
// g 中总共有 n 行
// 每行总共有 n 个元素,每个元素默认为 false,未有任何连接
g.push_back(std::vector<bool>(n, false));
}
}
~DenseGraph() {
}
/**
* 图中有多少顶点
*
* @return 顶点的个数
*/
int v() {
return n;
}
/**
* 图中有多少边
*
* @return 边的个数
*/
int e() {
return m;
}
/**
* 连接 v 和 w,在他们之间建立一条边
*
* 平行边:v 和 w 都是唯一的,不存在平行边
* 自环边:当 v 和 w 一样时,稠密图天生只会存在一个自环边
*/
void addEdge(int v, int w) {
assert(v >= 0 && v < n);
assert(w >= 0 && w < n);
if (hasEdge(v, w)) {
// 已经存在边了,重复的连接操作
return;
}
g[v][w] = true;
if (!directed) {
// 无向图
g[w][v] = true;
}
++m;
}
/**
* 两顶点之间是否存在边
*
* 时间复杂度:O(1)
*/
bool hasEdge(int v, int w) {
assert(v >= 0 && v < n);
assert(w >= 0 && w < n);
return g[v][w];
};
};稀疏图
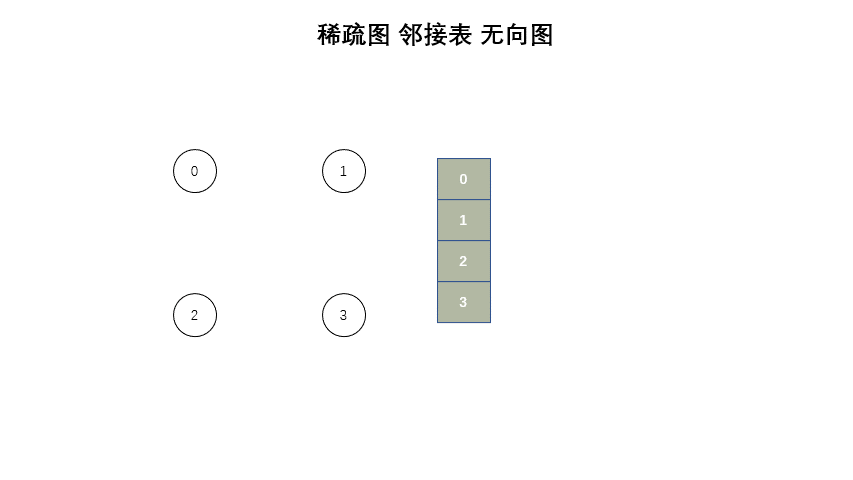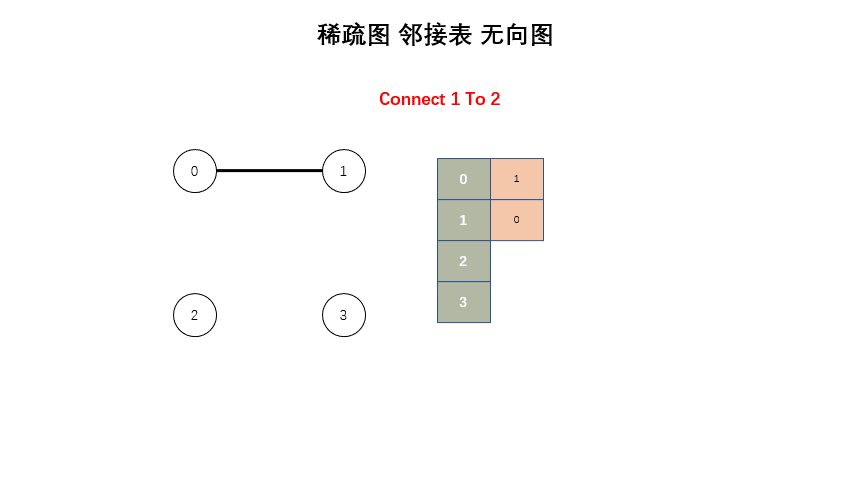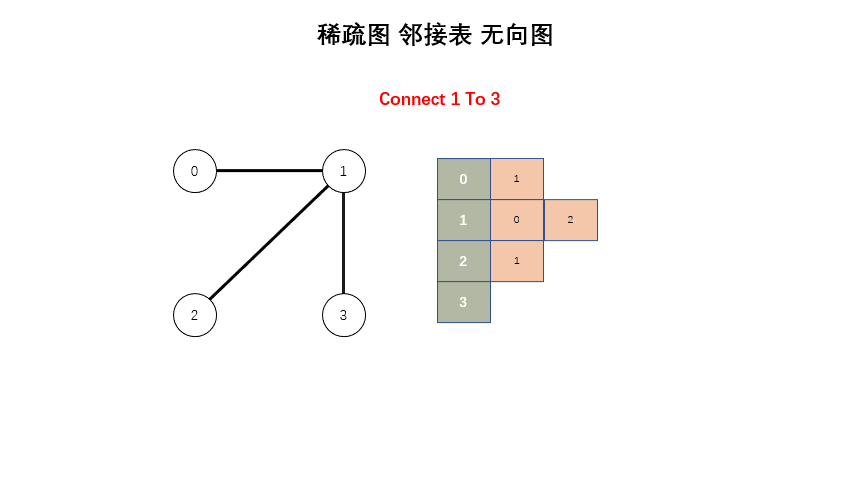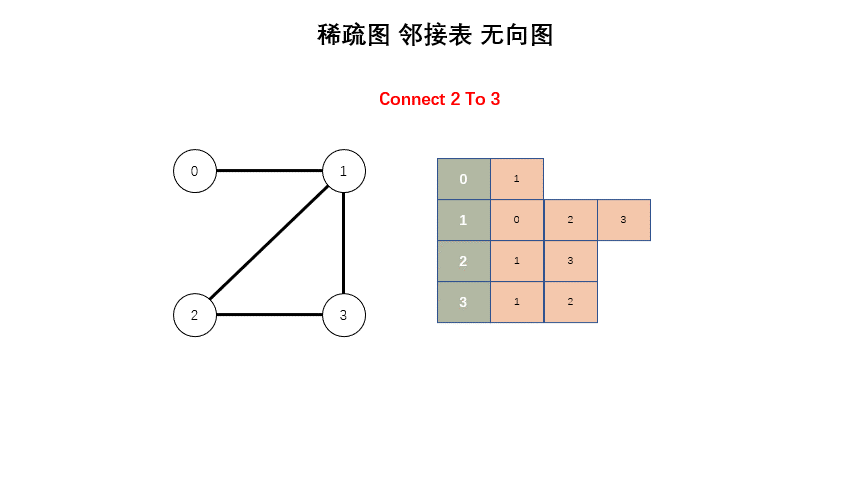
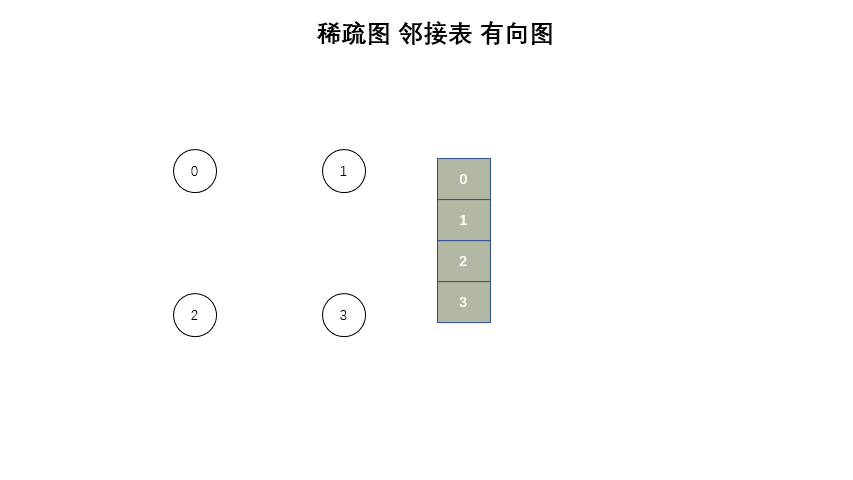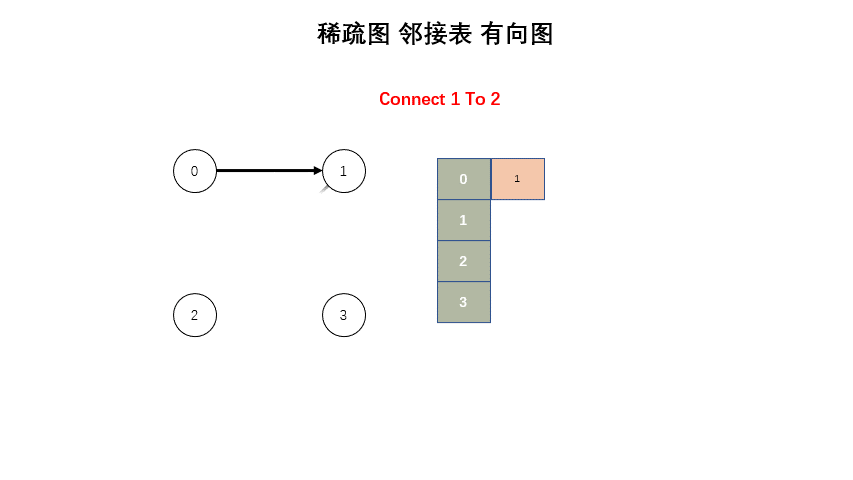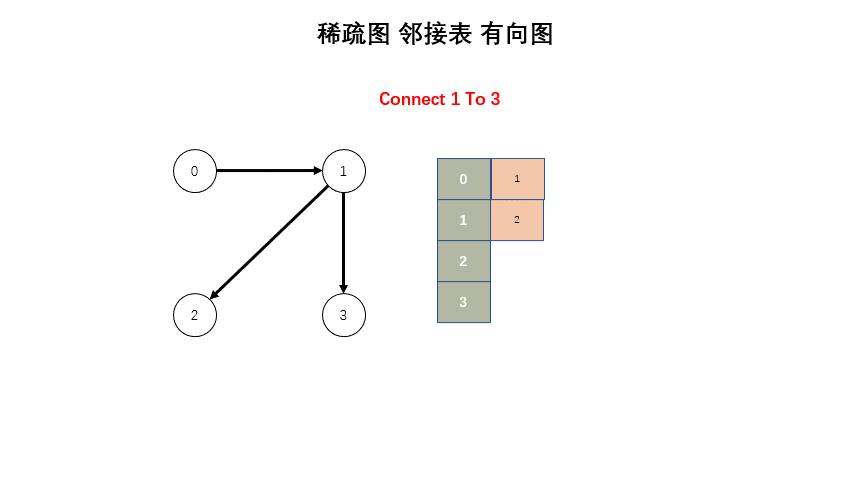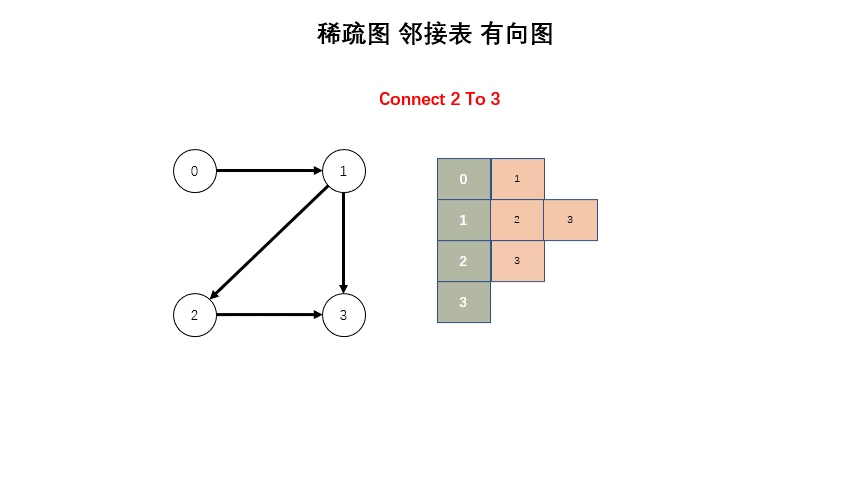
#include <iostream>
#include <cassert>
#include <vector>
/**
* 稀疏图 - 邻接表
*/
class SparseGraph {
private:
/**
* 图中顶点数、边数
*/
int n, m;
/**
* 是否为有向图
*/
bool directed;
/**
* 邻接表,每行存放的都是当前行所连接的所有顶点
*/
std::vector<std::vector<int>> g;
public:
SparseGraph(int n, bool directed) {
this->n = n;
this->m = 0;
this->directed = directed;
g = std::vector<std::vector<int>>(n, std::vector<int>());
}
~SparseGraph() {
}
/**
* 图中有多少顶点
*
* @return 顶点的个数
*/
int v() {
return n;
}
/**
* 图中有多少边
*
* @return 边的个数
*/
int e() {
return m;
}
/**
* 连接 v 和 w,在他们之间建立一条边
*
* 平行边:存在平行边的情况,如果添加的时候想过滤平行边,就需要调用 hasEdge 进行判断,那 addEdge 就变成了 O(n) 时间复杂度
* 一般不在 addEdge 时处理,在所有边都添加完毕之后再去重。
* 自环边:当 v 和 w 一样时,并且是无向图时,就会存在添加两次自环边的情况,所以要判断筛选掉
*/
void addEdge(int v, int w) {
assert(v >= 0 && v < n);
assert(w >= 0 && w < n);
g[v].push_back(w);
if (v != w && !directed) {
// 无向图
g[w].push_back(v);
}
++m;
}
/**
* 两顶点之间是否存在边
*
* 时间复杂度:O(n)
*/
bool hasEdge(int v, int w) {
assert(v >= 0 && v < n);
assert(w >= 0 && w < n);
for (int i = 0; i < g[v].size(); ++i) {
if (g[v][i] == w) {
return true;
}
}
return false;
}
};遍历邻边
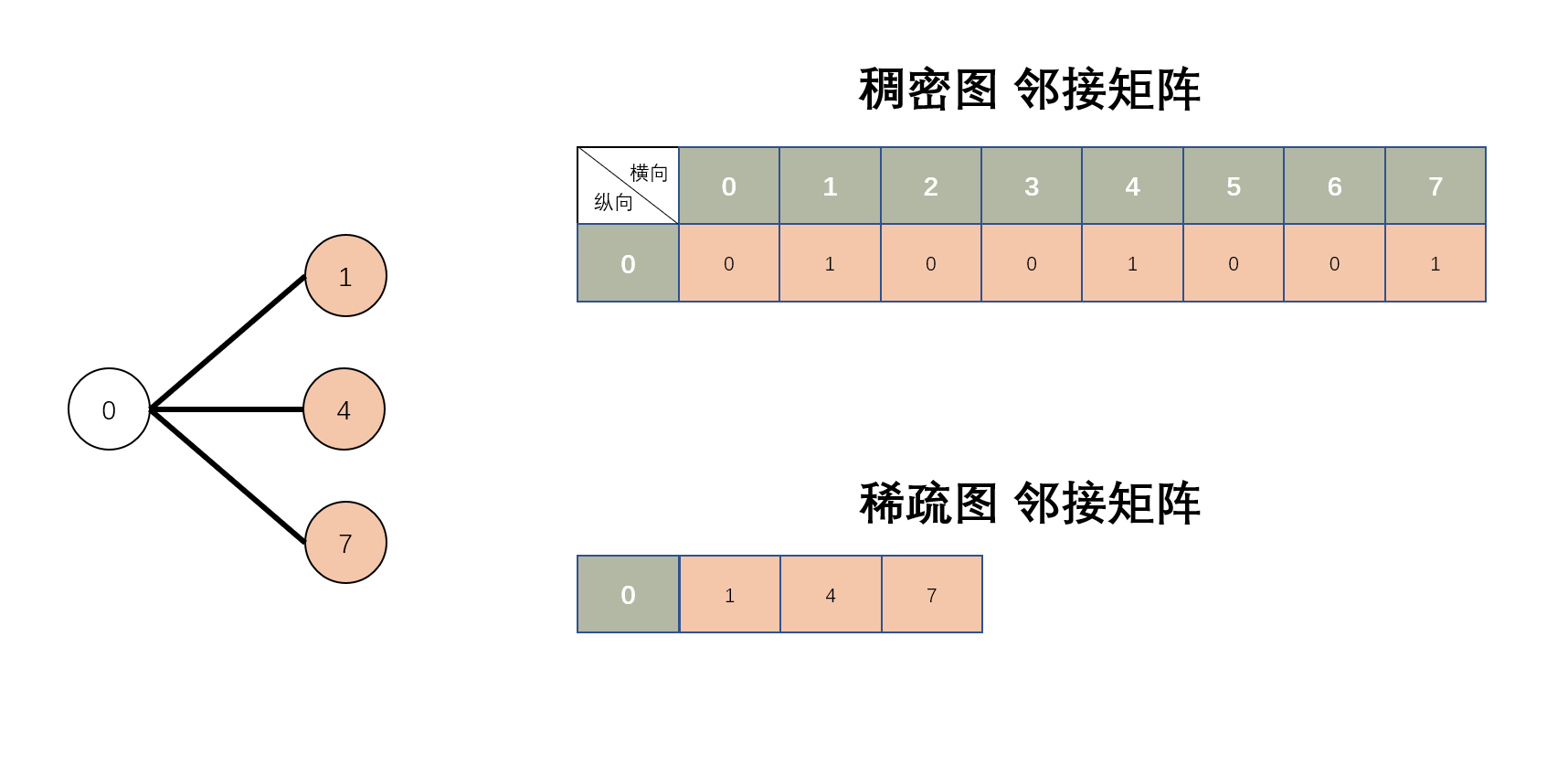
假设遍历 0 的邻边 1、4、7,如果是稠密图,就需要遍历整个 n 的长度,为 true 的是 0 的邻边。如果是稀疏图则可直接遍历,遍历出来的都是 0 的邻边。而大多数业务场景下,很少有一个顶点能连接其他所有顶点的情况,也就是使用稠密图的情况较少见,多数为使用稀疏图,稀疏图的遍历也更加有效率。
迭代器的形式实现
稠密图
/**
* 邻边迭代器
*/
class AdjIterator {
private:
DenseGraph &G;
/** 顶点 */
int v;
/** 当前迭代到第几个 */
int index;
public:
AdjIterator(DenseGraph &graph, int v) : G(graph) {
this->v = v;
this->index = 0;
}
/**
* 稠密图中,每一行的第 0 个元素不一定是相连的,要为 true 才为相连
*/
int begin() {
index = -1;
return next();
}
int next() {
// 只要 index 还小于顶点总数(稠密图中行和列数都是顶点总数),就可以继续向下查询
for (index += 1; index < G.v() ; ++index) {
if (G.g[v][index]) {
return index;
}
}
return -1;
}
bool end() {
return index >= G.v();
}
};稀疏图
/**
* 邻边迭代器
*/
class AdjIterator {
private:
SparseGraph &G;
/** 顶点数 */
int v;
/** 当前迭代到第几个 */
int index;
public:
AdjIterator(SparseGraph &graph, int v) : G(graph) {
this->v = v;
this->index = 0;
}
int begin() {
index = 0;
// size 大于 0
if (G.g[v].size()) {
return G.g[v][index];
}
return -1;
}
int next() {
++index;
if (index < G.g[v].size()) {
return G.g[v][index];
}
return -1;
}
bool end() {
return index >= G.g[v].size();
}
};测试
void vertexAdjTraverseByDenseGraph() {
int n = 20;
int m = 100;
// Dense Graph
// 创建一张稠密图
DenseGraph graph(n, false);
// 随机让两个顶点进行相连
for (int i = 0; i < m; i++) {
int a = rand() % n;
int b = rand() % n;
graph.addEdge(a, b);
}
// 时间复杂度: O(V^2)
for (int v = 0; v < n; v++) {
std::cout << v << " : ";
DenseGraph::AdjIterator adj(graph, v);
for (int w = adj.begin(); !adj.end(); w = adj.next())
std::cout << w << " ";
std::cout << std::endl;
}
std::cout << std::endl;
}
void vertexAdjTraverseBySparseGraph() {
int n = 20;
int m = 100;
srand(time(NULL));
// Sparse Graph
// 创建一张稀疏图
SparseGraph graph(n, false);
// 随机让两个顶点进行相连
for (int i = 0; i < m; i++) {
int a = rand() % n;
int b = rand() % n;
graph.addEdge(a, b);
}
// 时间复杂度: O(E),E 为边的总数
for (int v = 0; v < n; v++) {
std::cout << v << " : ";
SparseGraph::AdjIterator adj(graph, v);
for (int w = adj.begin(); !adj.end(); w = adj.next())
std::cout << w << " ";
std::cout << std::endl;
}
std::cout << std::endl;
}
int main() {
// 测试稠密图遍历所有顶点的邻边
vertexAdjTraverseByDenseGraph();
// 测试稀疏图遍历所有顶点的邻边
vertexAdjTraverseBySparseGraph();
return 0;
}打印结果:
稠密图所有顶点的邻边遍历
0 : 3 5 12 13 16 17 19
1 : 4 5 6 7 10 11 15 16
2 : 9 12 14 15 17 19
3 : 0 5 6 8 9 10 11 12 15 16
4 : 1 13 14 16
5 : 0 1 3 9 10 12 13 15 17
6 : 1 3 10 15 16 17
7 : 1 10 11 13 14
8 : 3 10 14
9 : 2 3 5 9 11 14 15
10 : 1 3 5 6 7 8 10 16 17 18 19
11 : 1 3 7 9 12 13 15 16 19
12 : 0 2 3 5 11 14 19
13 : 0 4 5 7 11 13 15 16 17 18
14 : 2 4 7 8 9 12 16 17 18 19
15 : 1 2 3 5 6 9 11 13 16 17
16 : 0 1 3 4 6 10 11 13 14 15 17
17 : 0 2 5 6 10 13 14 15 16 19
18 : 10 13 14
19 : 0 2 10 11 12 14 17
稀疏图所有顶点的邻边遍历
0 : 19 16 13 5 17 12 3
1 : 16 10 11 15 7 4 11 5 6
2 : 12 19 17 15 14 9
3 : 8 16 9 12 5 10 5 6 5 11 0 15 15
4 : 13 1 16 14
5 : 12 3 17 3 9 9 1 3 13 0 15 10 12 13
6 : 16 10 17 15 16 16 10 3 1
7 : 10 10 14 13 11 1
8 : 3 10 14
9 : 3 11 9 5 14 2 5 11 15
10 : 18 16 6 10 8 1 7 18 3 7 6 10 19 5 17
11 : 19 13 9 12 19 1 19 7 12 16 1 12 3 19 15 9 16
12 : 5 2 3 19 11 14 11 11 0 5
13 : 15 18 11 4 17 13 16 16 7 0 5 5
14 : 12 7 2 9 17 8 18 19 19 4 16
15 : 13 17 6 2 1 16 5 11 3 9 3
16 : 1 6 3 10 6 6 13 15 13 0 11 4 17 14 11
17 : 6 15 2 13 5 19 14 0 16 10
18 : 13 10 10 14
19 : 11 2 12 11 11 0 17 11 10 14 14
进程已结束,退出代码0可以看到,稠密图的邻边关系,天然按顺序排放,并且不会出现平行边。而稀疏图是随机排放,会出现平行边。
从文件中读取图
准备好一个两个问题件 testG1.txt、testG2.txt 文件 ,如下:
testG1.txt
13 13
0 5
4 3
0 1
9 12
6 4
5 4
0 2
11 12
9 10
0 6
7 8
9 11
5 3
testG2.txt
6 8
0 1
0 2
0 5
1 2
1 3
1 4
3 4
3 5第一行第一个数字代表有多少个顶点,第一行第二个数字代表有多少条边。第二行的两个数字代表让对应的两个顶点相连,后续行与第二行一样。
创建读取类,采用模板类,兼容稠密图和稀疏图
#include <iostream>
#include <string>
#include <fstream>
#include <sstream>
#include <cassert>
using namespace std;
/**
* 从文件中读取图
*
* @tparam Graph 读取的图采用模板类,兼容稠密图、稀疏图
*/
template<typename Graph>
class ReadGraph {
public:
ReadGraph(Graph &graph, const string &filename) {
// 打开文件
ifstream file(filename);
string line;
// 顶点和边数
int v, e;
assert(file.is_open());
// 获取第一行
assert(getline(file, line));
stringstream ss(line);
// 读取顶点数 和 边数
ss >> v >> e;
// 顶点数要对应
assert(v == graph.v());
for (int i = 0; i < e; ++i) {
assert(getline(file, line));
stringstream ss(line);
int a, b;
ss >> a >> b;
assert(a >= 0 && a < v);
assert(b >= 0 && b < v);
graph.addEdge(a, b);
}
}
};图类中增加 show 方法
/******** 稠密图 ********/
/**
* 显示图的信息
*/
void show() {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
std::cout << g[i][j] << "\t";
}
std::cout << std::endl;
}
}
/******** 稀疏图 ********/
/**
* 显示图的信息
*/
void show() {
for (int i = 0; i < n; i++) {
std::cout << "vertex " << i << ":\t";
for (int j = 0; j < g[i].size(); j++) {
std::cout << g[i][j] << "\t";
}
std::cout << std::endl;
}
}测试
void readGraph() {
string filename = "testG1.txt";
SparseGraph g1(13, false);
ReadGraph<SparseGraph> readGraph(g1, filename);
cout<<"test G1 in Sparse Graph:" << endl;
g1.show();
cout<<endl;
DenseGraph g2( 13 , false );
ReadGraph<DenseGraph> readGraph2( g2 , filename );
cout<<"test G1 in Dense Graph:" << endl;
g2.show();
cout<<endl;
// 使用两种图的存储方式读取 testG2.txt 文件
filename = "testG2.txt";
SparseGraph g3( 6 , false );
ReadGraph<SparseGraph> readGraph3( g3 , filename );
cout<<"test G2 in Sparse Graph:" << endl;
g3.show();
cout<<endl;
DenseGraph g4( 6 , false );
ReadGraph<DenseGraph> readGraph4( g4 , filename );
cout<<"test G2 in Dense Graph:" << endl;
g4.show();
}
int main() {
readGraph();
return 0;
}
文章评论