二叉堆
简介
二叉堆(英语:binary heap)是一种特殊的堆,二叉堆是完全二叉树。二叉堆满足堆特性:父节点的键值总是保持固定的序关系于任何一个子节点的键值,且每个节点的左子树和右子树都是一个二叉堆。
当父节点的值总是大于或等于任何一个子节点的值时为「最大堆」。当父节点的值总是小于或等于任何一个子节点的值时为「最小堆」。
完全二叉树:一棵深度为 k 的有 n 个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为 i (1 ≤ i ≤ n)的结点与满二叉树中编号为 i 的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。
若设二叉树的深度为 h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,比如第一层下面最大数是两个节点,第二层下面最大数是四个节点;第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
二叉堆的作用
可以完全理解二叉堆之后再来看其作用
-
用作
Priority Queue。 -
把多个有序容器里面的元素合并到一个大的有序容器里面(类似归并排序的变种)。假设有 n 个有序容器,我们希望把这些容器里面的元素有序地放到一个大容器里面去。我们姑且称 n 个有序容器为小容器。对每个小容器维护一个 cursor,cursor 刚开始指向小容器中的第一个元素,即最小的元素。每个循环中,对 n 个 cursor 指向的 n 个元素建立一个最小堆;从这个堆里面 extract 最小的元素加到大容器里面;被 extract 最小元素的那个小容器的 cursor 往后挪一位;进入下一个循环。如果一个容器的 cursor 到达end了,那么最小堆的大小减一。因为我们每次加入到大容器里面的都是当前所有小容器中最小的元素,所以大容器是有序的。
-
寻找 n 个数里面最大的 m 个数。比如 n = 2000万、m = 100。可以先将 2000 万个元素,拆分成 2000 组,每组 1 万个元素。每组用这 1 万个元素,进行建堆,注意,建立最小堆,建一个大小为 100 的堆。后续的数据进堆之后先看看是否比堆顶的数据小,如果小,就直接跳过,继续下一个,否则就把堆顶的移除掉,新数据入堆,并调整堆顺序。这样,就得到了 2000 个大小为 100 的堆。之后就需要把这 2000 个堆进行分组合并掉,最红只剩下一个大小为 100 的堆。
实现一个二叉堆(最大二叉堆)
二叉堆的特性
二叉堆一般使用数组、索引从 1 开始的方式实现,最大二叉堆父节点必然比两个子节点大。通过上图也可以发现,在父找子、子找父中有两个公式。
子找父:子索引 / 2
父找子:左子:父索引 * 2。右子:父索引 * 2 + 1
如果数组是从 0 开始,那公式为:
子找父:(子索引 - 1) / 2
父找子:左子:父索引 * 2 + 1。右子:父索引 * 2 + 2
经典的做法是从数组索引 1 的位置开始。
二叉堆基础结构

template<typename Item>
class MyMaxHeap {
private:
// 堆数据
Item *data;
// 堆容量
int capacity;
// 堆数量统计
int count;
public:
explicit MyMaxHeap(int capacity) {
// 由于堆数据的索引从 1 开始,相当于会浪费一个索引为 0 的空间。
// 所以调用者如果想开辟一个长度为 capacity 的对数据空间,那这里还需要 +1 个,才能符合调用者的预期。
data = new Item[capacity + 1];
this->capacity = capacity;
count = 0;
}
~MyMaxHeap() {
delete[] data;
}
int size() {
return count;
}
bool isEmpty() {
return count == 0;
}
};新增数据
在堆的最后位置进行新增数据,新增的数据有大有小,这是不确定,所以需要对新增的数据进行上浮操作,把新增的数据上浮到对应的索引位置。
先观察一下动画
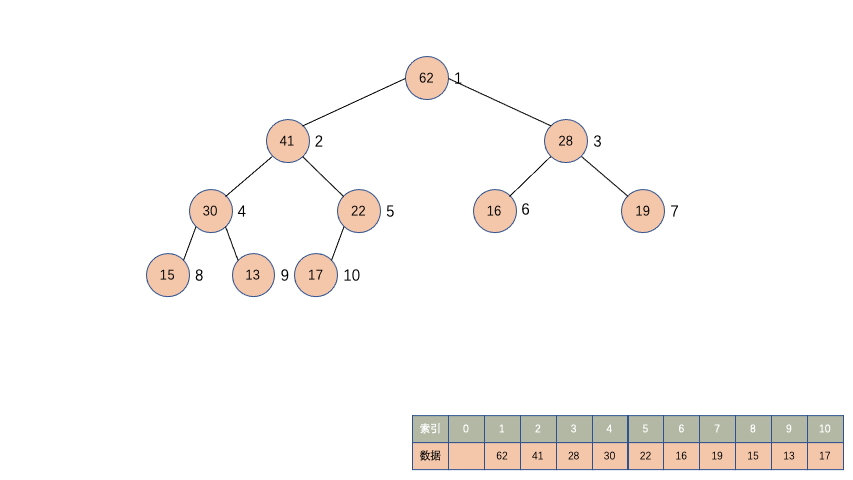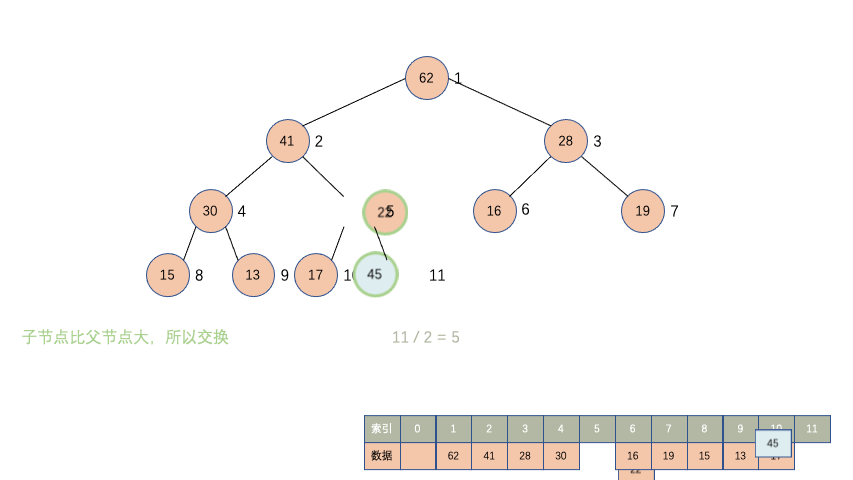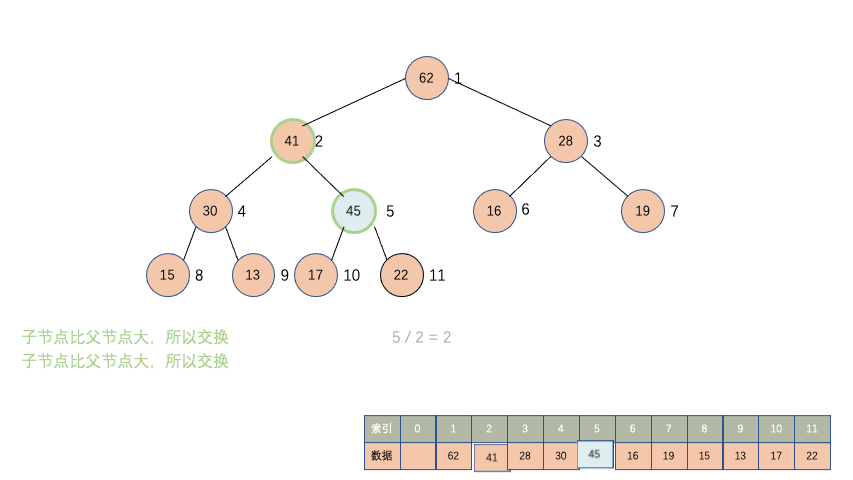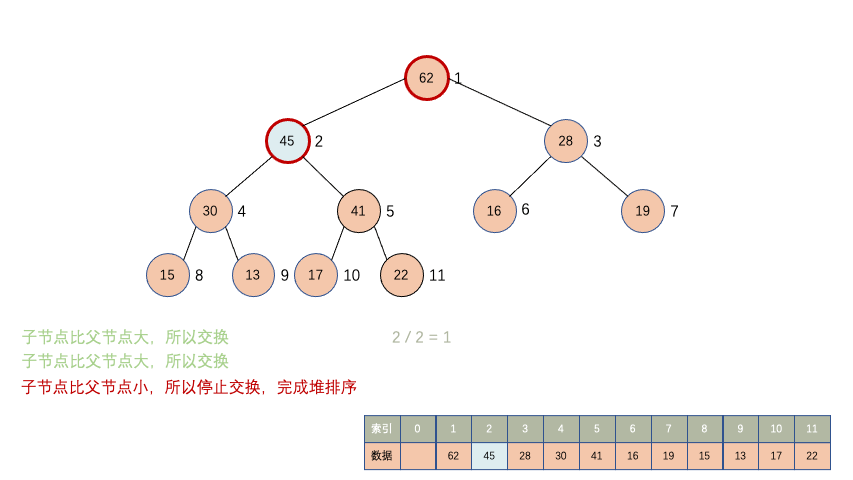
/**
* 上浮规则
* 1. idx 需要大于 1 才有意义。小于 1:不存在这种情况。等于 1:说明是第一个进堆的数据,不需要上浮了。
* 2. idx / 2 = 父节点所在索引
* 3. 与父节点作比较
* 父节点小,与父节点进行交换
* 把父节点的索引重新赋值给 idx,循环 2、3 步骤。
* 父节点大,上浮完毕
*
* @param idx 尝试要上浮数据所在堆数据索引。
*/
void shiftUp(int idx) {
while (idx > 1 && data[idx / 2] < data[idx]) {
swap(data[idx / 2], data[idx]);
idx = idx / 2;
}
}
/**
* 新增数据
*/
void insert(Item item) {
while (count >= capacity) {
// 空间不足了,扩充
Item *newData = new Item[capacity * 2 + 1];
// 数组索引为 0 的位置是不用的。
/*for (int i = 1; i <= count; ++i) {
newData[i] = data[i];
}*/
memcpy(newData + 1, data + 1, count * sizeof(Item));
delete[] data;
data = newData;
capacity *= 2;
}
// 新增数据放入末尾
data[count + 1] = item;
count += 1;
// 尝试上浮新增的数据
shiftUp(count);
}提取数据
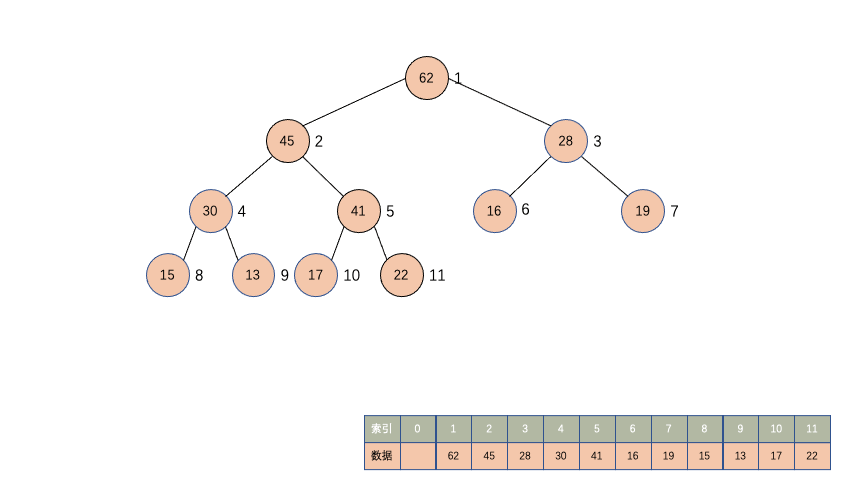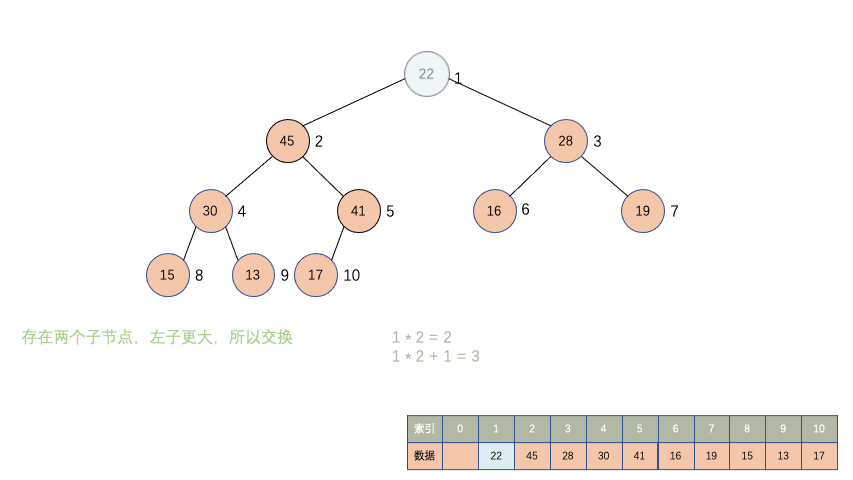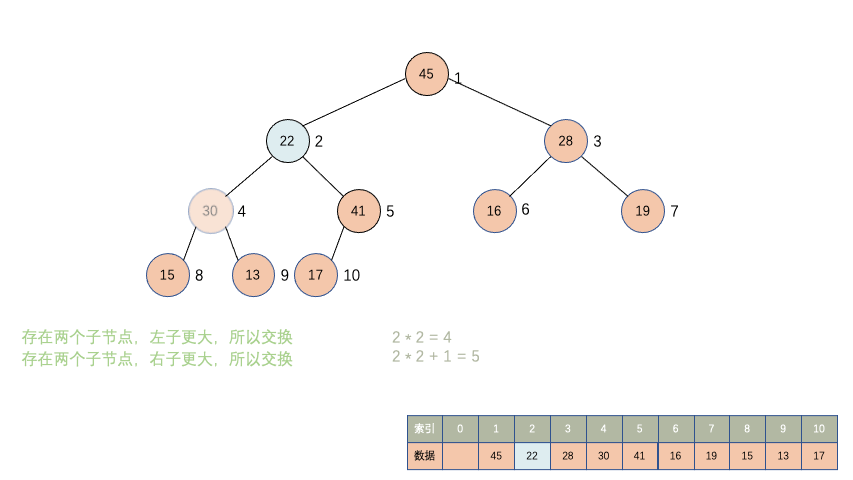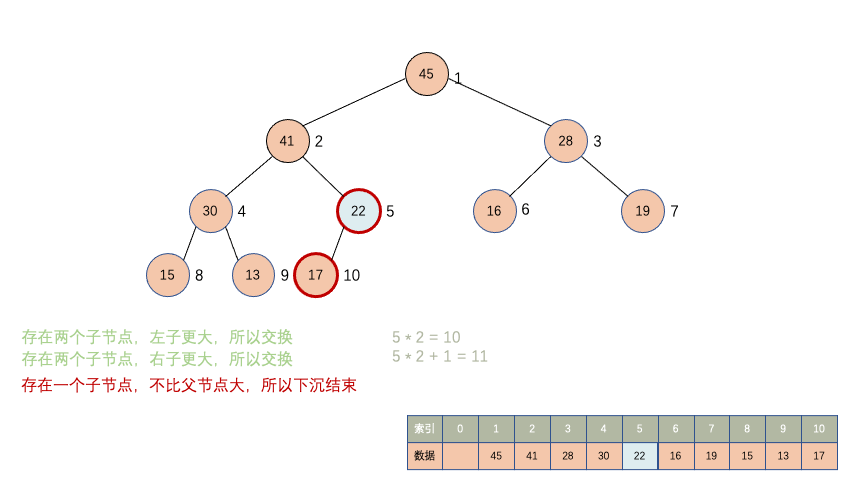
在堆中去数据就是把堆顶,也就是索引为 1 的数据取出来,然后把堆尾的数据放在堆顶,因为原来堆尾的数据大概率不是整个堆中最大的值,那现在却在堆顶的位置,所以还需要对其进行下沉操作,下沉到合适的索引。
先观察一下动画
/**
* 下沉规则
* 1. 至少存在一个左子节点
* 2. 若果存在右子节点,先想左右两个子节点进行进性比较出最大值。选定最大的子节点索引 dstIdx
* 3. 选定子节点如果比父节点大 就交换,否则就结束下沉
* 4. 交换之后父节点索引变成选定子节点的索引继续 1 循环步骤
*
* @param idx 尝试要下沉数据所在堆数据索引。
*/
void shiftDown(int idx) {
while (idx * 2 <= count) {
// 存在子节点
int dstIdx = idx * 2;
if ((dstIdx + 1) <= count && data[dstIdx] < data[dstIdx + 1]) {
// 存在右子节点并且右子节点比 左子节点 大
dstIdx = dstIdx + 1;
}
// 直接点不能比父节点大
if (data[idx] >= data[dstIdx]) {
break;
}
swap(data[idx], data[dstIdx]);
idx = dstIdx;
}
}
/**
* 提取数据
*
* @return 因为是最大堆,所以每次都是提取堆中最大的数据
*/
Item extractMax() {
assert(count > 0);
Item result = data[1];
data[1] = data[count];
count--;
shiftDown(1);
return result;
}索引堆
上面实现了一个简单的最大堆,同时也发现了两个问题
- 数据入堆之后想修改一下某个数据的优先级就变得比困难,因为入堆后的数据索引已经完全乱掉了,与外部调用认为的索引是不一样的。
- 数据入堆、提取都会伴随有
swap操作,如果只是小数据还好,如果是大的结构体、类、字符串,那开销就相当大了。
引入索引数组
之前在上浮、下沉做完比较之后,直接交换数组 data 不同索引对应的值,这样的交换方式,笼统上来说堆索引越小索引对应的值是越大的,堆索引 0 位置的值是最大。这种数据结构好处就是直观、便于理解,但是会出现上面那两个问题,为了解决上面的问题,引入一个新的数组 indexes,这个数组中存储的数据为堆索引,在进行上浮、下沉的过程中,堆数据 data 就不变了,变的是这个 indexes 中的堆索引。如下图:
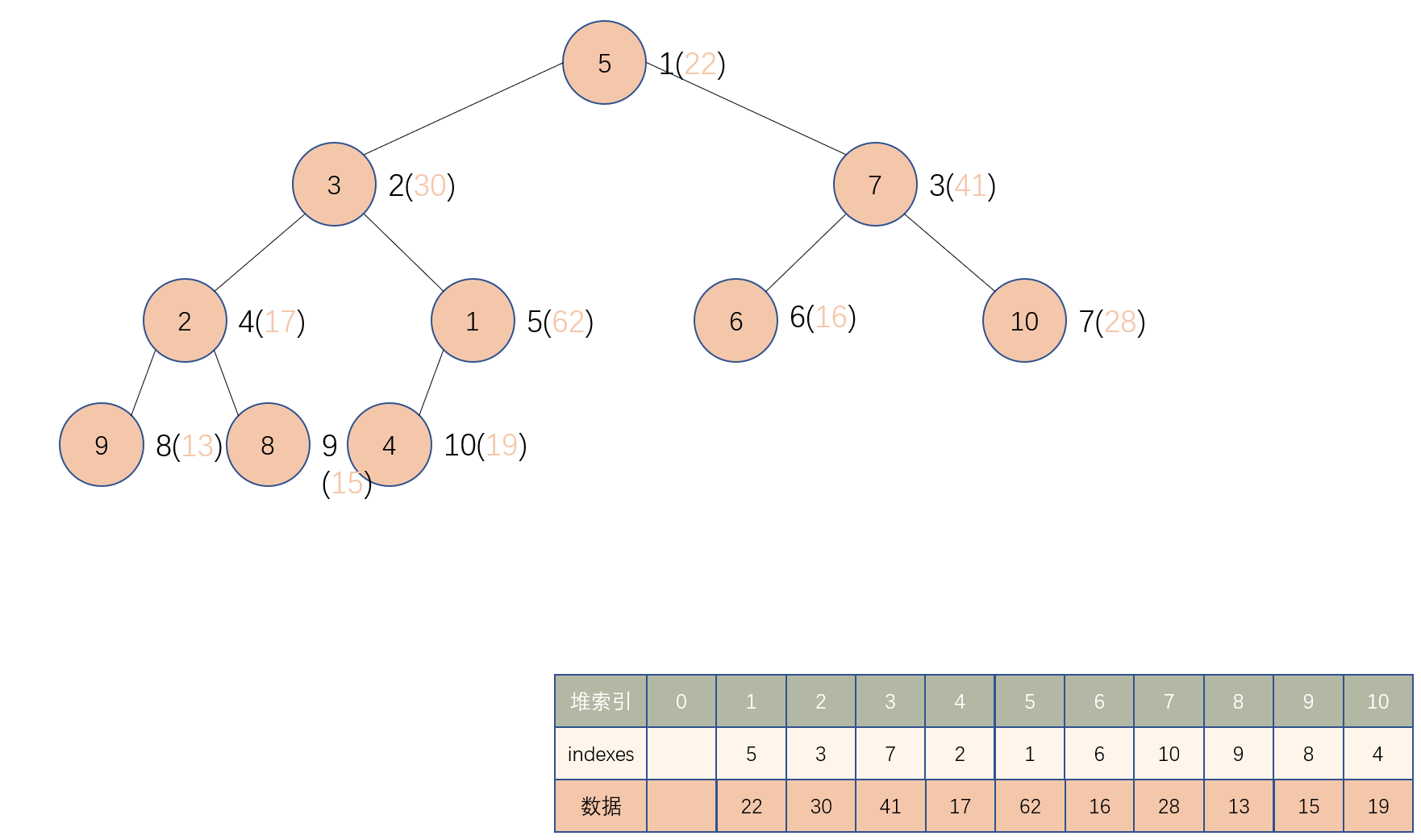
在引入索引堆概念之前,堆索引 1所对应的数据就是最大的值,堆索引 与 数据相互对应,数据会在上浮、下沉过程中不断交换,而引入索引堆概念之后,数据不会变了,变的只有 indexes,indexes 中每个索引所存储的就是 堆索引,通过上图也可以看到,交换的全都是 indexes 中的堆索引,而数据就和堆索引牢牢对应着,不会改变了,这样一来,外界调用如果想修改一个数据,只需要传入对应的索引即可。而仅仅只是交换 indexes 中的堆索引值,开销上就会小很多了。在引入堆索引之前,data 的索引就是堆索引,而引入堆索引之后,indexes 的索引才是堆索引。
引入堆索引之前:通过 data 的索引直接取得 data 中的数据,就是符合堆数据结构的排列组合。
引入堆索引之后:通过堆索引从 indexes 中取得真正堆结构中的堆索引,进而通过 data 才能取得对应的堆中数据。
更改之后就外界调用者就可以方便的获取指定索引的数据也可以修改指定索引的数据。
修改后代码:
//
// Created by lynch on 2022/5/25.
//
#ifndef CPLUSPLUS_MY_MAX_HEAP_H
#define CPLUSPLUS_MY_MAX_HEAP_H
template<typename Item>
class MyMaxHeap {
private:
// 堆数据
Item *data;
// 堆中的索引
int *indexes;
// 堆容量
int capacity;
// 堆数量统计
int count;
/**
* 上浮规则
* 1. idx 需要大于 1 才有意义。小于 1:不存在这种情况。等于 1:说明是第一个进堆的数据,不需要上浮了。
* 2. idx / 2 = 父节点所在索引
* 3. 与父节点作比较
* 父节点小,与父节点进行交换
* 把父节点的索引重新赋值给 idx,循环 2、3 步骤。
* 父节点大,上浮完毕
*
* @param idx 尝试要上浮数据所在堆数据索引。
*/
void shiftUp(int idx) {
while (idx > 1 && data[indexes[idx / 2]] < data[indexes[idx]]) {
swap(indexes[idx / 2], indexes[idx]);
idx = idx / 2;
}
}
/**
* 下沉规则
* 1. 至少存在一个左子节点
* 2. 若果存在右子节点,先想左右两个子节点进行进性比较出最大值。选定最大的子节点索引 dstIdx
* 3. 选定子节点如果比父节点大 就交换,否则就结束下沉
* 4. 交换之后父节点索引变成选定子节点的索引继续 1 循环步骤
*
* @param idx 尝试要下沉数据所在堆数据索引。
*/
void shiftDown(int idx) {
while (idx * 2 <= count) {
// 存在子节点
int dstIdx = idx * 2;
if ((dstIdx + 1) <= count && data[indexes[dstIdx]] < data[indexes[dstIdx + 1]]) {
// 存在右子节点并且右子节点比 左子节点 大
dstIdx = dstIdx + 1;
}
// 直接点不能比父节点大
if (data[indexes[idx]] >= data[indexes[dstIdx]]) {
break;
}
swap(indexes[idx], indexes[dstIdx]);
idx = dstIdx;
}
}
public:
explicit MyMaxHeap(int capacity) {
// 由于堆数据的索引从 1 开始,相当于会浪费一个索引为 0 的空间。
// 所以调用者如果想开辟一个长度为 capacity 的对数据空间,那这里还需要 +1 个,才能符合调用者的预期。
data = new Item[capacity + 1];
indexes = new int[capacity + 1];
this->capacity = capacity;
count = 0;
}
~MyMaxHeap() {
delete[] data;
delete[] indexes;
}
int size() {
return count;
}
bool isEmpty() {
return count == 0;
}
/**
* 新增数据
*/
void insert(int srcIdx, Item item) {
// 外界传入的索引从 0 开始,堆内部从 1 开始,所以需要 +1
srcIdx += 1;
// count + 1: 接下来要再用一个空间,所以如果 +1 超过了 capacity,就需要扩容了
// srcIdx: 外界的对应堆中的索引如果超过 capacity 说明需要扩容了
while (count + 1 > capacity || srcIdx > capacity) {
// 空间不足了,扩充
Item *newData = new Item[capacity * 2 + 1];
// 数组索引为 0 的位置是不用的。
/*for (int i = 1; i <= count; ++i) {
newData[i] = data[i];
}*/
memcpy(newData + 1, data + 1, count * sizeof(Item));
delete[] data;
data = newData;
int *newIndexes = new int[capacity * 2 + 1];
memcpy(newIndexes + 1, indexes + 1, count * sizeof(int));
delete[] indexes;
indexes = newIndexes;
capacity *= 2;
}
// 新增数据放入末尾
data[srcIdx] = item;
indexes[count + 1] = srcIdx;
count += 1;
// 尝试上浮新增的数据
shiftUp(count);
}
/**
* 提取数据
*
* @return 因为是最大堆,所以每次都是提取堆中最大的数据
*/
Item extractMax() {
assert(count > 0);
Item result = data[indexes[1]];
indexes[1] = indexes[count];
count--;
shiftDown(1);
return result;
}
/**
* 提取数据索引
*
* @return 因为是最大堆,所以每次都是提取堆中最大的索引
*/
int extractMaxIdx() {
assert(count > 0);
int result = indexes[1];
indexes[1] = indexes[count];
count--;
shiftDown(1);
return result;
}
/**
* 获取堆中指定索引的数据
*
* @param srcIdx 指定索引
*/
Item getItem(int srcIdx) {
// 外界传入的索引从 0 开始,堆内部从 1 开始,所以需要 +1
srcIdx += 1;
assert(srcIdx >= 1 && srcIdx <= capacity);
return data[srcIdx];
}
/**
* 修改指定索引数据
*
* @param srcIdx 指定索引
*/
void change(int srcIdx, Item newItem) {
// 外界传入的索引从 0 开始,堆内部从 1 开始,所以需要 +1
srcIdx += 1;
data[srcIdx] = newItem;
// 由于修改了原来的,那么此值对应的索引在 indexes 中就不一定是正确的了
// 所以需要找到其索引在 indexes 中的位置,并对 indexes 索引进行的上浮、下沉操作。
for (int i = 1; i <= count; ++i) {
if (indexes[i] == srcIdx) {
shiftUp(i);
shiftDown(i);
return;
}
}
}
};
#endif //CPLUSPLUS_MY_MAX_HEAP_H
文章评论