二分查找
基础二分实现查找实现与动画

template<typename T>
int binarySearch(T arr[], int len, T target) {
int l = 0, r = len - 1;
while (l <= r) {
// 求中值
int mid = l + ((r - l) >> 1);
if (arr[mid] == target) {
return mid;
}
if (arr[mid] > target) {
r = mid - 1;
} else {
l = mid + 1;
}
}
return -1;
}
int main() {
int arr[10] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
cout <<"The binarySearch index is :" << binarySearch(arr, 10, 5) << endl;
return 0;
}The binarySearch index is: 4floor 和 ceil
假设有以下这样一个有序数组
int arr[10] = {1, 2, 3, 5, 5, 5, 7, 8, 9, 10};分别有以下两个查询需求
- 查找目标
5,如果存在或者存在多个,返回最左边的那个索引。否则返回比 5 小的最近的元素索引。(floor) - 查找目标
5,如果存在或者存在多个,返回最右边的那个索引。否则返回比 5 大的最近的元素索引。(ceil)
这两个需求与基本的二分查找是有区别的,如果是二分查找,第一下就找到索引 4 并返回,而这两个需求其实理想中返回的应该是 3 和 5
floor
根据 floor 的查找要求,可以能出现下面四种情况。
- 目标在数组中间某一段。
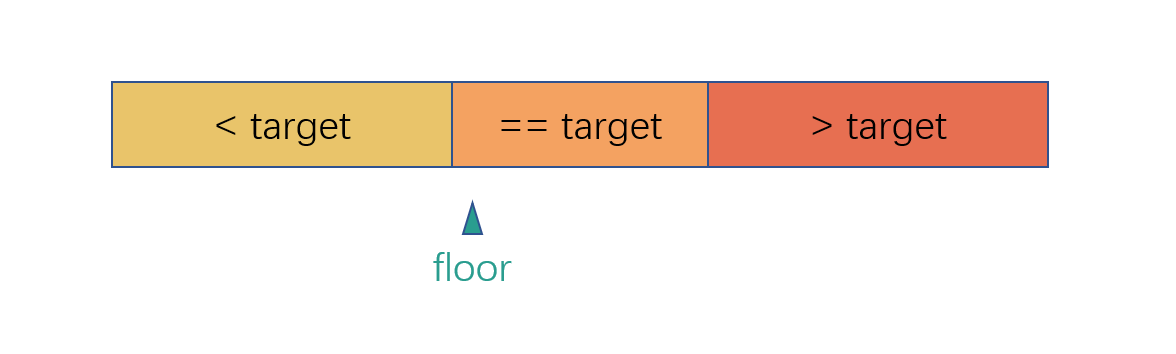
- 目标不存在,假如目标存在,其所在位置应该是在数组的中间,注意这里的中间是指非两端,而不是正中间。
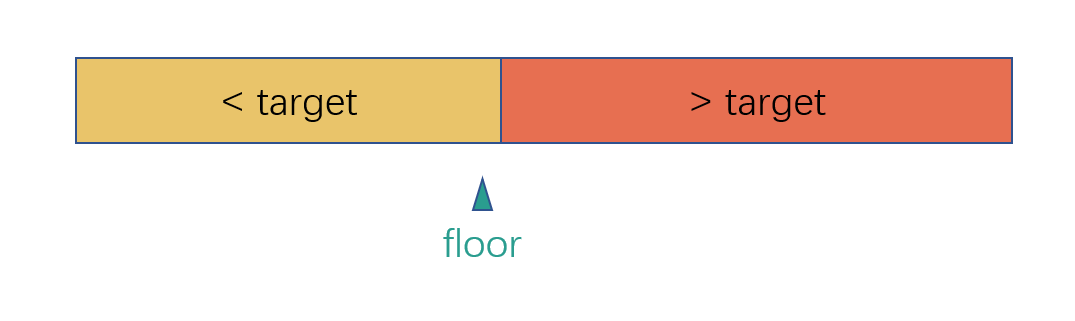
- 目标不存在,目标值比数组中所有值都小。

- 目标不存在,目标值比数组中所有值都大。

根据上图也可以看出,如果存在,就取最左边的索引,不存在,就取理论上最靠近目标值左边的索引。根据图也可以查看 floor 的取值范围应该是 [-1, len - 1],左闭右闭区间,数组中不存在目标值并且所有值都比目标值大时,floor = -1,数组中不存在目标值并且所有值都比目标值小时,floor = len - 1。
代码实现如下:
template<typename T>
int floor(T arr[], int len, T target) {
int l = -1, r = len - 1;
while (l < r) {
// 使用向上取整避免死循环
int mid = l + ((r - l + 1) >> 1);
if (target <= arr[mid]) {
r = mid - 1;
} else {
l = mid;
}
}
if (l + 1 < len && arr[l + 1] == target) {
return l + 1;
} else {
return l;
}
}死循环问题
代码中有一点需要注意,int mid = l + ((r - l + 1) >> 1);,一般情况下取中值都是常规写法是 l + ((r - l) >> 1),这里的写法是还做了 +1 操作,先不说为啥,先来看看 l + ((r - l) >> 1) 有什么问题。
代码中的循环条件是 l < r,那么 r - l 的值肯定是大于 0 的。再细分一下可以分为两种。
- r - l = 1;
- r - l > 1;
先把 r - l = 1 的情况代入到 mid = l + ((r - l) / 2) 中。
// 化简
mid = l + ((r - l) / 2)
// 因前面代入的 是 r - l = 1,所以 (r - l) 为奇数,比如 r=3、l=2 时。在计算机除法运算中,一个奇数 / 2 = (这个奇数 - 1) 除以 2,如 3 / 2 = 1、2 / 2 = 1。
// 那么上式可得
mid = l + ((r - l - 1) / 2)
mid = l + (0 / 2)
mid = l;把 r - l = 1 的情况代入到 mid = l + ((r - l) / 2) 中最后得出的结果是 mid = l,这时如果是走的 else 分支,也就是 target > arr[mid] 的情况,就会执行 l = mid;mid 等于 l,l 又等于 mid,下一次循环 l 的值并没有变,继续循环,结果就是在进行一次上边的推到,就 死循环 了。
那如果把 r - l > 1 的情况代入 mid = l + ((r - l) / 2) 中呢
// 化简
mid = l + ((r - l) / 2)
// 这里简单认为 r - l = 2 吧。
mid = l + 1;
// r - l = 2 的情况最终 mid 都等于 l + 1 了,那 更大的情况只会是 l 加的值更大,所以更不会有问题上边得到 mid = l + 1,这时如果是走的 else 分支,也就是 target > arr[mid] 的情况,就会执行 l = mid,相当于 l = l + 1,所以 l 的值变了,继续循环条件判断。
死循环的关键点
推导了一通之后发现存在两个关键点
- r - l = 1 的时候,l 的值是不会增加的。
- else 中 l 的赋值语句不像普通的二分查找那样,进行 +1。
先看第二个关键点,为了保持 floor 的算法逻辑,不太好动。那就看第一个关键点能不能改。
思考之后发现 r - l = 1 会造成死循环的原因是这个 1 / 2 = 0,这种是计算机计算中默认的取值方式,向下取整;1 / 2 = 0、5 / 2 = 2 等等都是向下取整,1 / 2 = 0 导致在表达式 l + ((r - l) / 2) 中 l 最后只能加个 0,那走到 else 之后就相当于没变过,所以死循环。那就让 1 / 2 不等于 0,让它等于 1,这样最终 l 就是加个 1 了,就不会死循环了。一切的一切就在 r - l = 1 的这个节点上,这里把表达式 l + ((r - l) >> 1) 更改成 l + ((r - l + 1) >> 1) 之后,及时 r - l = 1,在除以 2 之前会再 +1,就变成了 2,2 / 2 = 1,进而表达式最左边的 l 就可以 +1 了,哪怕走 else 逻辑也不会死循环了。这种做法就是向上取整。
改完之后的式子:int mid = l + ((r - l + 1) >> 1);。在进行验算一下吧。
r - l > 1 的情况就不看了,本身就没问题,还把 r - l = 1 的情况代入进去。
mid = l + ((r - l + 1) / 2)
mid = 1 + ((1 + 1) / 2)
mid = l + 1;验证通过,更改之后没问题。

ceil
根据 ceil 的查找要求,可以能出现下面四种情况。
- 目标在数组中间某一段。
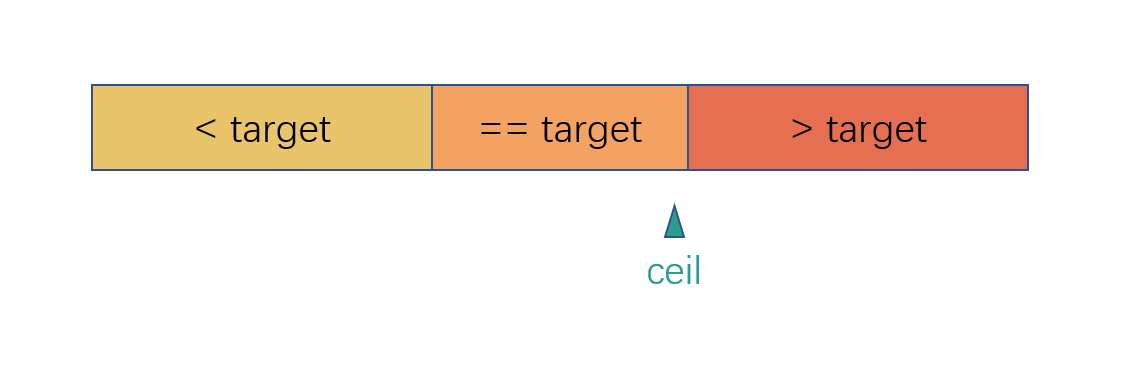
- 目标不存在,假如目标存在,其所在位置应该是在数组的中间,注意这里的中间是指非两端,而不是正中间。
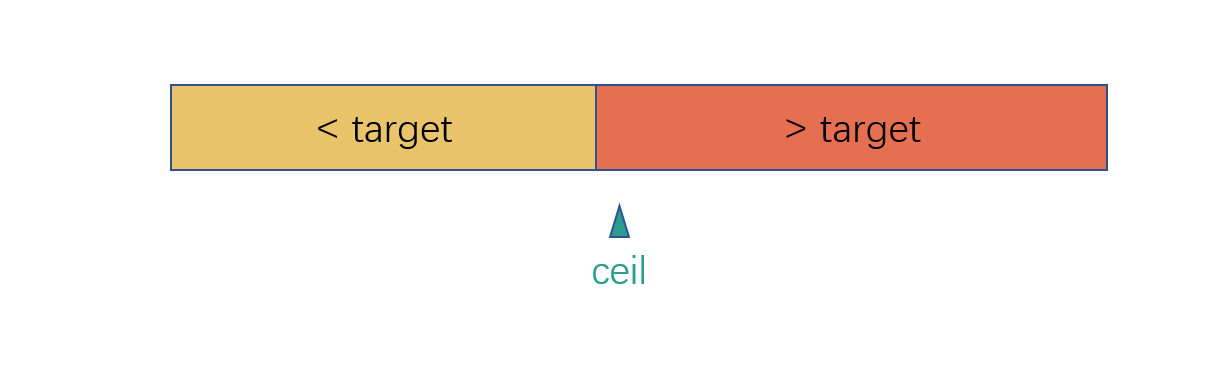
- 目标不存在,目标值比数组中所有值都小。

- 目标不存在,目标值比数组中所有值都大。

根据上图也可以看出,如果存在,就取最右边的索引,不存在,就取理论上最靠近目标值右边的索引。根据图也可以查看 ceil 的取值范围应该是 [0, len],左闭右闭区间,数组中不存在目标值并且所有值都比目标值大时,ceil = 0,数组中不存在目标值并且所有值都比目标值小时,ceil = len。
代码实现如下:
template<typename T>
int ceil(T arr[], int len, T target) {
int l = 0, r = len;
while (l < r) {
// 使用普通的向下取整即可避免死循环
int mid = l + ((r - l) >> 1);
if (target >= arr[mid]) {
l = mid + 1;
} else {
r = mid;
}
}
if (r - 1 > 0 && arr[r - 1] == target) {
return r - 1;
} else {
return r;
}
}ceil 不会存在死循环问题,floor 存在是因为下届值 l 是直接复制 mid,又碰到除法默认向下取整的情况。而 ceil,是使用上届值 r,这时候默认除法向下取整,恰巧让 r 进行了 -1 操作。
简单记就是看到 l = mid,r = mid - 1 的时候需要向上取整。
文章评论