基本页面布局 Scaffold 中有个 ListView,ListView 中有 100 个高 50 的 Container 用作辅助观看,ListView 中第三个元素是一个 GridView,GridView 的滑动效果被禁止。 class GiveView extends GetView<GiveController> { const GiveView({Key? key}) : super(key: key); @override Widget build(BuildContext contex…
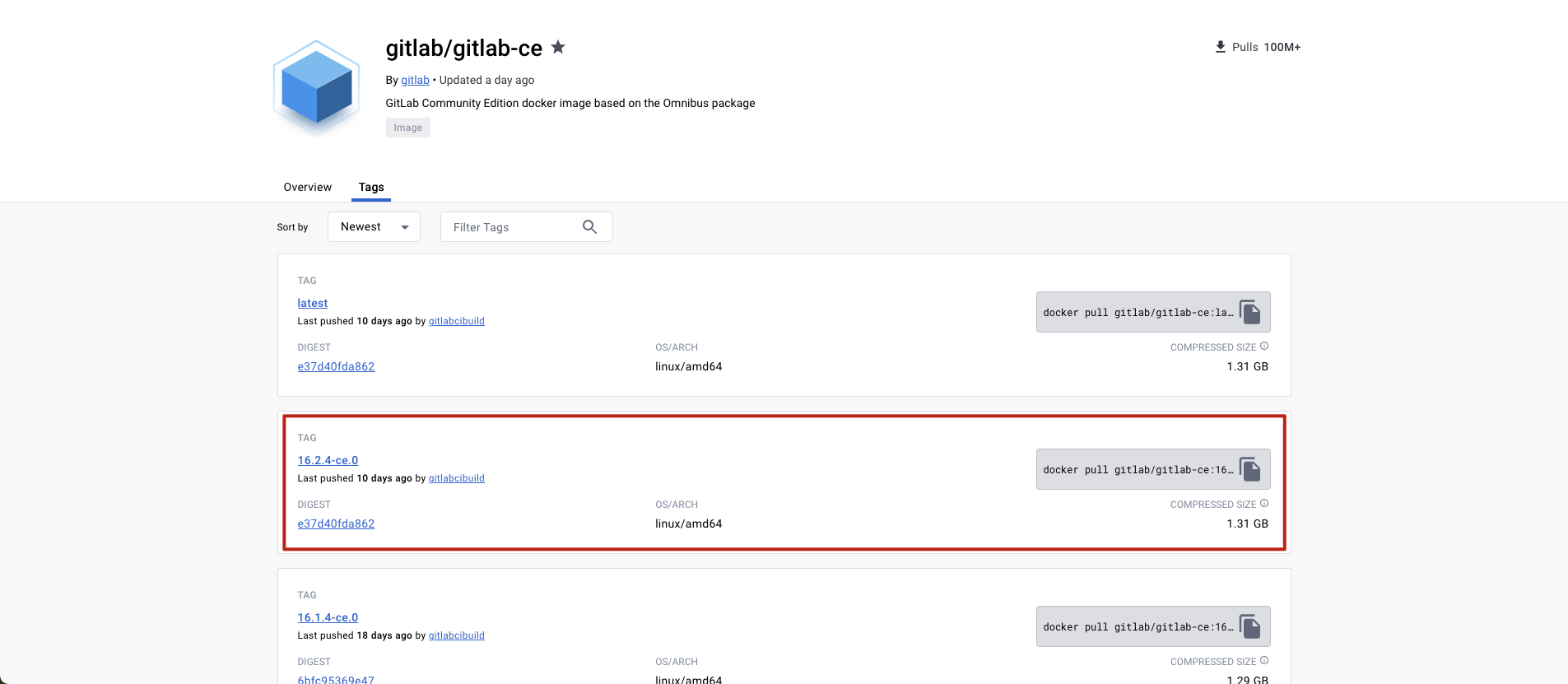
Version:gitlab-ce:16.2.4-ce.0 简介 Gitlab 是一个开源的 Git 代码仓库系统,可以实现自托管的 Github 项目,即用于构建私有的代码托管平台和项目管理系统。系统基于 Ruby on Rails 开发,速度快、安全稳定。它拥有与 Github 类似的功能,能够浏览源代码,管理缺陷和注释。可以管理团队对仓库的访问,它非常易于浏览提交过的版本并提供一个文件历史库。团队成员可以利用内置的简单聊天程序(Wall)进行交流。它还提供一个代码片段收集功能可以轻松实现代码复用,便于日后有需…
参数说明 环境变量 描述 值示例 http_proxy 为 http 变量设置代理;默认不填开头以http协议传输。 192.168.22.2:1080br>user:password@192.168.22.2:1080
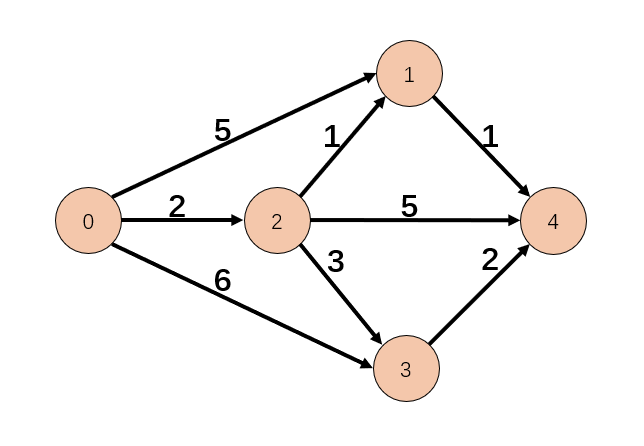
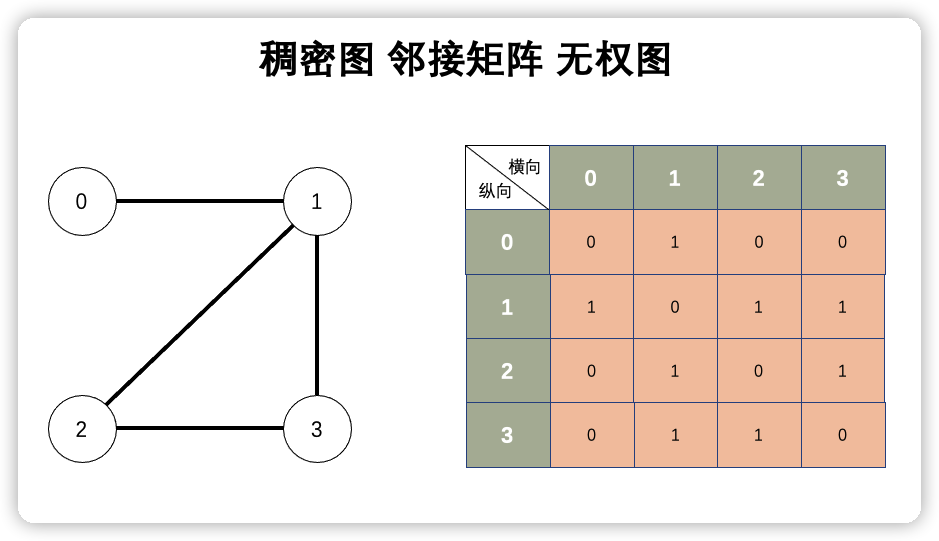
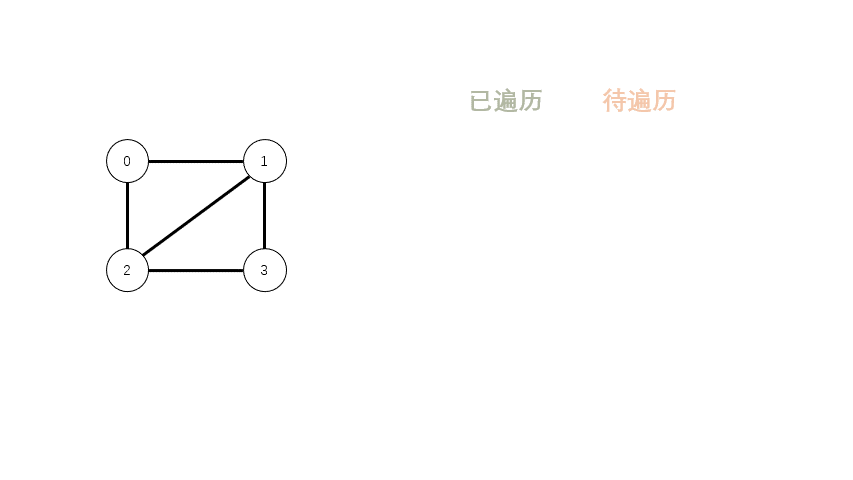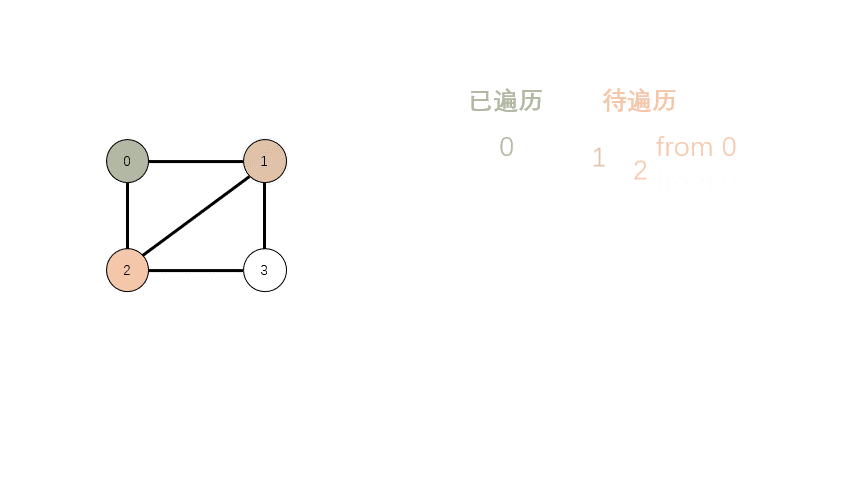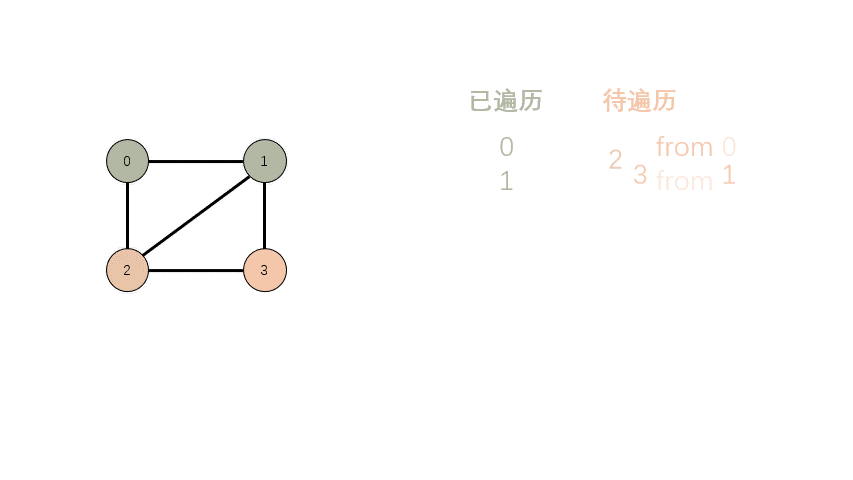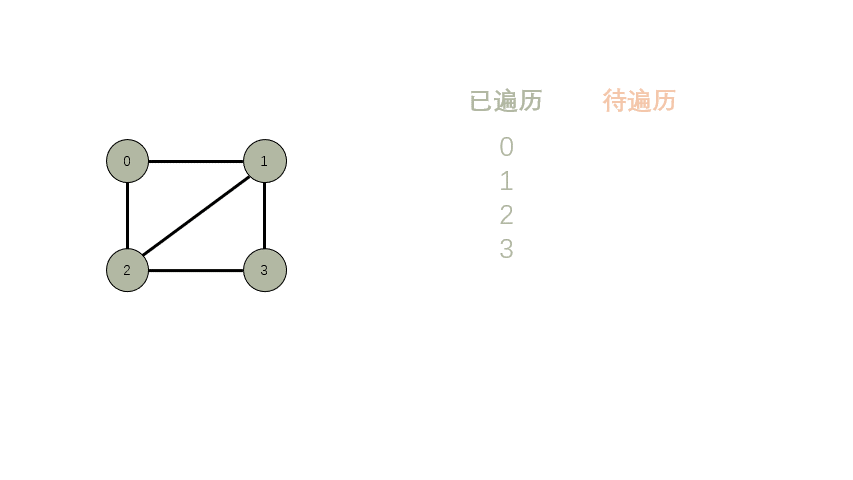
简介 迪杰斯特拉算法(Dijkstra) 是由荷兰计算机科学家狄克斯特拉于1959年提出的,因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法,解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始,采用贪心算法的策略,每次遍历到始点距离最近且未访问过的顶点的邻接节点,直到扩展到终点为止。 注意,Dijkstra 算法无法处理负权边的情况,比如 0 到 2 点的距离为:-2。 松弛操作(Relaxation) 何为松弛操作,文字描述比较抽象,看图吧。 0 的邻点有 1、2、3,距离分别是 5…
Kruskal Kruskal 是一个简单、易于理解的算法,效率比 Prim 低,对要求不高的场景可以使用。 先把所有边进行排序(从小到大),开始遍历。 从遍历中挨个从小到大取出边,如果这条边被选为了最小生成树,是否会形成环? 如果会形成环就不能选定这条边。不能形成环,那就可以选定为最小生成树中的一员。 直至循环结束。 循环也可以不必到最后一个索引,只需判断选中边达到 点数 - 1 即可。 以上的关键点在于要判断两点之间的边如果被选中了,是否会形成环?这里可以使用 Union Find 在遍历的过程中把已经相连的点…
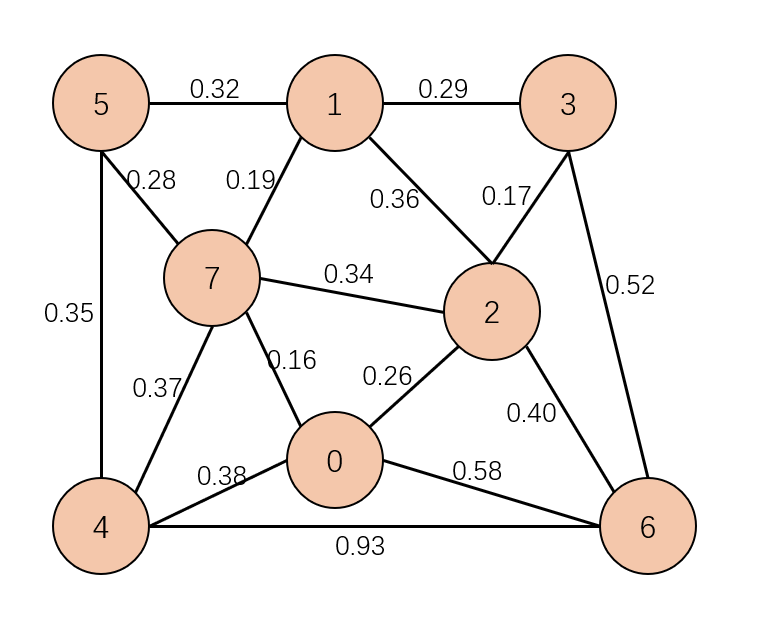
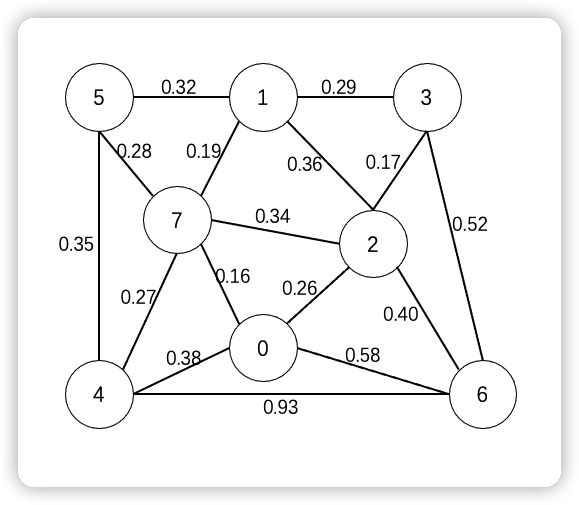
简介 什么是最小生成树?假设有 N 个点,通过 N - 1 条边将它们相连接,就叫做生成树,而最小就是这 N - 1 条边的权重相加最小,综合起来就是最小生成树。 下面一张图: 按照最小生成树的规则,最终可以找到这样一条线: 0-7、7-5、5-4、7-1、0-2、2-3、2-6 7 条边把所有的点进行相连,形成了这张图的最小生成树。在这里也能看出来,想要找最小生成树,这个图必须是一个连通图,也就是没有其他的连通分量。 切分定理(Cut Property) 那通过什么样的方式可以求得总共有哪些边可以组成最小生成树?…